接續著上一回,我們已經有一個單層的Neurel Network,緊接著我們來試著一步一步改造它,讓它成為我們常使用的Deep Neurel Network的形式。
本單元程式碼可於Github下載。
| import random
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
tf.logging.set_verbosity(tf.logging.ERROR)
# Config the matplotlib backend as plotting inline in IPython
%matplotlib inline
|
增加Hidden Layer
在上一回當中,我們只有一層Neurel Network,也就是做完一個線性轉換後,就直接使用Softmax Layer來轉換成機率表示方式,這樣的結構並不夠powerful,我們需要把它的結構弄的又窄又深,這樣效果才會好,詳細原因請參考這一篇的介紹。
因此,我們來試著加入一層Hidden Layer,來打造成兩層的Neurel Network,並在兩層之間加入Activation Function,為我的Model增加非線性因子。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28 | def structure(self, features, labels, n_hidden, activation, dropout_ratio=0, train=False):
# build neurel network structure and return their predictions and loss
### Variable
if (not self.weights) or (not self.biases):
self.weights = {
'fc1': tf.Variable(tf.truncated_normal(shape=(self.n_features, n_hidden))),
'fc2': tf.Variable(tf.truncated_normal(shape=(n_hidden, self.n_labels))),
}
self.biases = {
'fc1': tf.Variable(tf.zeros(shape=(n_hidden))),
'fc2': tf.Variable(tf.zeros(shape=(self.n_labels))),
}
### Structure
# layer 1
fc1 = self.getDenseLayer(features, self.weights['fc1'],
self.biases['fc1'], activation=activation)
if train:
fc1 = tf.nn.dropout(fc1, keep_prob=1-dropout_ratio)
# layer 2
logits = self.getDenseLayer(fc1, self.weights['fc2'], self.biases['fc2'])
y_ = tf.nn.softmax(logits)
loss = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits))
return (y_, loss)
|
首先在變數需要有二層的fully-connect參數,注意這些參數的大小,受到Hidden Layer的神經元數目n_hidden決定。接下來開始建構整個Neurel Network的結構,fc1產生一個fully-connect的結果,並且通過Activation Function再輸出,然後進到下一層,第二層直接使用fc1的結果當作新的輸入,再做一次fully-connect,並且讓它通過Softmax Layer來完成最後的Logistic轉換,它的loss一樣的是使用cross-entropy來評估。
Activation Function的選擇
剛剛提到的Hidden Layer可以採用不同的Activation Function,我列幾個常使用的Activation Function給大家看看。
| with tf.Session() as sess:
x = np.linspace(-3, 3)
tanh = tf.nn.tanh(x).eval()
sigmoid = tf.nn.sigmoid(x).eval()
relu = tf.nn.relu(x).eval()
plt.plot(x,tanh, 'g', x,sigmoid, 'b', x,relu, 'r')
plt.legend(('tanh', 'sigmoid', 'relu'))
plt.show()
|

這些Activation Function的使用時機可以簡單這樣說,當我們想要輸出值在+1和-1之間時使用tanh,而當我們想要一個輸出值衡為正時使用sigmoid,它可以將輸出值壓在+1和0之間。tanh比sigmoid多了兩個好處,第一,tanh的梯度變化大於sigmoid,有利於訓練效率,第二,tanh的輸出均值為0,可以避免將前層的梯度偏差帶到下一層。
不過,以上的這兩種Activation Function在非常深的網路都會有一個共通問題—梯度消失,仔細看上圖,tanh和sigmoid在極大和極小的地方都會彎成平的,所以每過一次這種Activation Function,訊號就會減小一點,當我們在深網路做Backpropagation時,訊號在過程中不斷的被磨損,到了前面的幾層就已經耗損完畢,此時更新的梯度近乎0,也就是梯度消失,那麼前面的這些層就再也訓練不到了。
Relu正可以解決梯度消失的問題,如上圖,在正的部分Relu是線性的,所以多少訊號進來就多少訊號出去,如此一來就不會有耗損的問題,但特別注意,因為tanh和sigmoid會將輸出值限制在一個範圍內,所以有Normalization的味道,但是Relu沒有限制,Normalization可以使我們訓練的效率提升(因為梯度的方向可以直指低點),所以Relu常常會搭配Normalization Layer一起使用,來額外做Normalization,或者是最近一篇Paper提到的一種新的Activation Function:SELU,類似於Relu但是輸出值會是Normalize過的,非常神奇,在這邊我不多論述。
Mini-Batch Gradient Descent
在上一回當中,我們的Gradient Descent採用的是將所有的Data一次全考慮進去,評估完所有的Data在一次性的更新權重參數,這樣的作法好處是比較穩定,因為我考慮的是真正的Training Set的\(E_{in}\),但缺點就是計算時間長,因為要考慮所有Training Set的每筆數據,需要做大矩陣的計算,而且通常Training Set的數據量也不可以太小,這麼一來計算時間就會拉的很長。
因此,有另外一種作法一次只考慮「一筆」數據,使用一筆數據來評估並更新權重參數,每一筆雖然更新結果都不怎麼準確,但是當我隨著時間看過整個Training Set後,就會有平均的效果,所以最後只要Learning Rate不要太大,最後的結果還是可以朝向最佳解的,這個手法會使得Gradient Descent具有隨機性,因此又被稱為Stochastic Gradient Descent,它所帶來的優點是計算時間變短了,我們將可以避免去涉及大矩陣的運算,但缺點是一次只評估一筆數據,將會非常的不穩定。
另外還有一種介於Gradient Descent和Stochastic Gradient Descent之間的作法,稱之為Mini-Batch Gradient Descent,它不像Stochastic Gradient Descent那麼極端,一次只評估一組Data,Mini-Batch Gradient Descent一次評估k組數據,並更新參數W,這是相當好的折衷方案,平衡計算時間和更新穩定度,而且在某些情形下,計算時間還比Stochastic Gradient Descent還快,為什麼呢?GPU的架構設計是非常有利於矩陣計算的,因為GPU會利用它強大的平行化將矩陣運算中每個元素平行計算,可以大大增進效率,所以如果一次只算一筆資料,反而是沒有利用到GPU的效率,所以如果你用GPU計算的話,依照你的GPU去設計適當的k值做Mini-Batch Gradient Descent,這個k值不要超過GPU平行計算所能容納的最大上限,這是個既有效率又更為穩定的作法,順道一提Tensorflow是可以支援GPU的計算的。
實務經驗告訴我們Mini-Batch Gradient Descent雖然穩定性比Gradient Descent差,但是收斂的速度卻一點都不輸給Gradient Descent,原因就出在更新的次數,Mini-Batch Gradient Descent一次看的數據筆數比較少,所以Mini-Batch一個Epoch可以更新參數好幾次,而Gradient Descent卻只能更新一次,Mini-Batch的靈敏性,使得它的收斂速度更為快速。打個比方,就好像是兩艘船在搜尋小島,Gradient Descent像是巡洋艦,它有更好設備可以有更好的觀測能力,但是因為它的笨重造成它反應不夠靈敏,Mini-Batch Gradient Descent就像是小船一樣,雖然觀測設備沒這麼好,但是反應靈敏,卻是可以更容易率先找到小島。
那我們來看看要怎麼做到Mini-Batch Gradient Descent。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23 | def fit(self, X, y, epochs=10, validation_data=None, test_data=None, batch_size=None):
...略...
self.sess.run(self.init_op)
for epoch in range(epochs):
print('Epoch %2d/%2d: ' % (epoch+1, epochs))
# mini-batch gradient descent
index = [i for i in range(N)]
random.shuffle(index)
while len(index) > 0:
index_size = len(index)
batch_index = [index.pop() for _ in range(min(batch_size, index_size))]
feed_dict = {
self.train_features: X[batch_index, :],
self.train_labels: y[batch_index],
}
_, loss = self.sess.run([self.train_op, self.loss], feed_dict=feed_dict)
print('[%d/%d] loss = %9.4f ' % (N-len(index), N, loss), end='\r')
...略...
|
在每一個epoch都完整的看過數據一遍,而mini-batch gradient descent是隨機取batch_size筆數據來更新權重,所以我採用這樣的作法,先依照數據的筆數N列出可能的Index有哪些,然後再做一個random.shuffle來做到隨機採樣,然後接下來只要簡單的從前面取batch_size筆數據進行更新,直到用盡所有的index為止,就可以做到mini-batch的效果。
Regularization
當你開始加深你的DNN時,就已經在增加Model的複雜度,增加複雜度想當然爾的可以增加對於數據的描述能力,在分類問題中代表可以增加精確度,不過要特別注意Overfitting的出現,當Model越複雜越容易產生Overfitting,Overfitting的結果是有看過的數據描述的很好,但沒看過的數據預測就很差,所以在Training的過程要特別注意Validation Set的表現,如果發現Training Set的表現越來越好,但是Validation Set的表現裹足不前甚至變的更差,那就很有可能已經Overfitting了。
如果你已經看到Overfitting出現了,有什麼方法可以抑制他呢?這個時候就需要Regularization的幫忙,在Neurel Network常見的Regularization有兩種:Weight Regularization和Dropout,待會會一一介紹。
這邊特別注意,不要每次精確度沒有提升就怪Overfitting!如果連你的Training Set都沒辦法有好的表現,這就可能不是Overfitting,反而可能是Underfitting,這個時候不要再增加Regularization,而是試著去調整Learning Rate,或者增加模型的複雜度,加深DNN或增加神經元的數目。
Weight Regularization
我們可以藉著在Loss Function裡頭加入Weight的貢獻,來達到限制W的大小的目標,這樣做可以降低Overfitting,詳細原理請參考這篇的Regularization的部分。
我們來看看應該怎麼做到L2 Regularization。
| # regularization loss
regularization = tf.reduce_mean([tf.nn.l2_loss(w) / tf.size(w, out_type=tf.float32) for w in self.weights.values()])
# total loss
loss = original_loss + alpha * regularization
|
在這裡我習慣將Loss對Weights的個數做平均,這有一個好處當我在調整神經元數目時,alpha可以不需要大動作調整。
Dropout
Dropout是Deep Learning常用的Regularization技巧,它的作法是在訓練的時候我先隨機把部份的神經元關閉,使用較少的神經元訓練,來達到Regularization的效果,最後在「推論」的時候再使用全部的神經元,我個人覺得這有Aggregation Model的味道,分別訓練出許多的sub-model再做Aggregation以達到截長補短的效果。
實作上有一些細節必須要注意,當我們關閉一些神經元時,也就是等於減少部份的貢獻量,所以我們需要依照相應比例來給予權重,以抵銷減少的部分。舉個例子,假設今天原本應該要輸出的值有十個,這十個值都是1,然後因為Dropout,變成五個1五個0的輸出,我們看到原本貢獻量因為Dropout一半而少一半,這樣並不合理,會導致我後面的Weights在更新的時候低估更新量,所以我們必須要將「沒被Dropout的部分」權重乘上一倍,才可以解決問題。因此,如果Dropout \(r\)倍的神經元,權重就要乘以\((1/r)\)倍,我們來看看Tensorflow怎麼做的。
| with tf.Session() as sess:
S = tf.constant([[1, 1, 1, 1, 1, 1, 1, 1],
[3, 3, 3, 3, 3, 3, 3, 3],
[5, 5, 5, 5, 5, 5, 5, 5]],tf.float32) # 3 Data, 8 dim. Score
print('Original S =')
print(S.eval())
S_drop = tf.nn.dropout(S,keep_prob=0.5) # dropout ratio = 1 - keep_prob = 0.5
print('Dropout S =')
print(S_drop.eval())
|
| Original S =
[[1. 1. 1. 1. 1. 1. 1. 1.]
[3. 3. 3. 3. 3. 3. 3. 3.]
[5. 5. 5. 5. 5. 5. 5. 5.]]
Dropout S =
[[ 2. 0. 0. 2. 0. 0. 2. 0.]
[ 0. 0. 6. 0. 0. 6. 0. 6.]
[10. 10. 10. 0. 10. 10. 10. 10.]]
|
我們看到因為dropout 0.5倍,所以輸出值權重乘上2倍,另外一提,Tensorflow的Dropout機制是隨機的,所以Drop out的比例會接近我們想要的比例,但不是絕對剛好。
那我要怎麼把Dropout放進去我的Model呢?特別注意,我們並不希望已經Training完的Model還有Dropout這一層,所以我在structure裡頭設計一個train的開關,當我在Training過程就把它打開,Dropout這一層就會被加進去,「推論」的時候就關閉,保持原有的神經元數量。
1
2
3
4
5
6
7
8
9
10
11
12
13 | def structure(self,features,labels,n_hidden,activation,dropout_ratio=0,train=False):
... 略 ...
# layer 1
fc1 = self.getDenseLayer(features,self.weights['fc1'], self.biases['fc1'], activation=activation)
if train:
fc1 = tf.nn.dropout(fc1, keep_prob=1-dropout_ratio)
# layer 2
logits = self.getDenseLayer(fc1, self.weights['fc2'], self.biases['fc2'])
... 略 ...
|
Optimizer的選擇
我們可以自由的替換我們想要使用的Optimizer。
| # define training operation
optimizer = tf.train.AdamOptimizer(learning_rate)
self.train_op = optimizer.minimize(self.loss)
|
在Tensorflow中目前有以下十種Optimizer供我們使用。
- tf.train.GradientDescentOptimizer
- tf.train.AdadeltaOptimizer
- tf.train.AdagradOptimizer
- tf.train.AdagradDAOptimizer
- tf.train.MomentumOptimizer
- tf.train.AdamOptimizer
- tf.train.FtrlOptimizer
- tf.train.ProximalGradientDescentOptimizer
- tf.train.ProximalAdagradOptimizer
- tf.train.RMSPropOptimizer
如果想要了解每個Optimizer的演算法可以參考這篇有詳細的說明。
來看看程式怎麼寫
講了那麼多,來看看完整的程式怎麼寫?照慣例,先畫個流程圖。
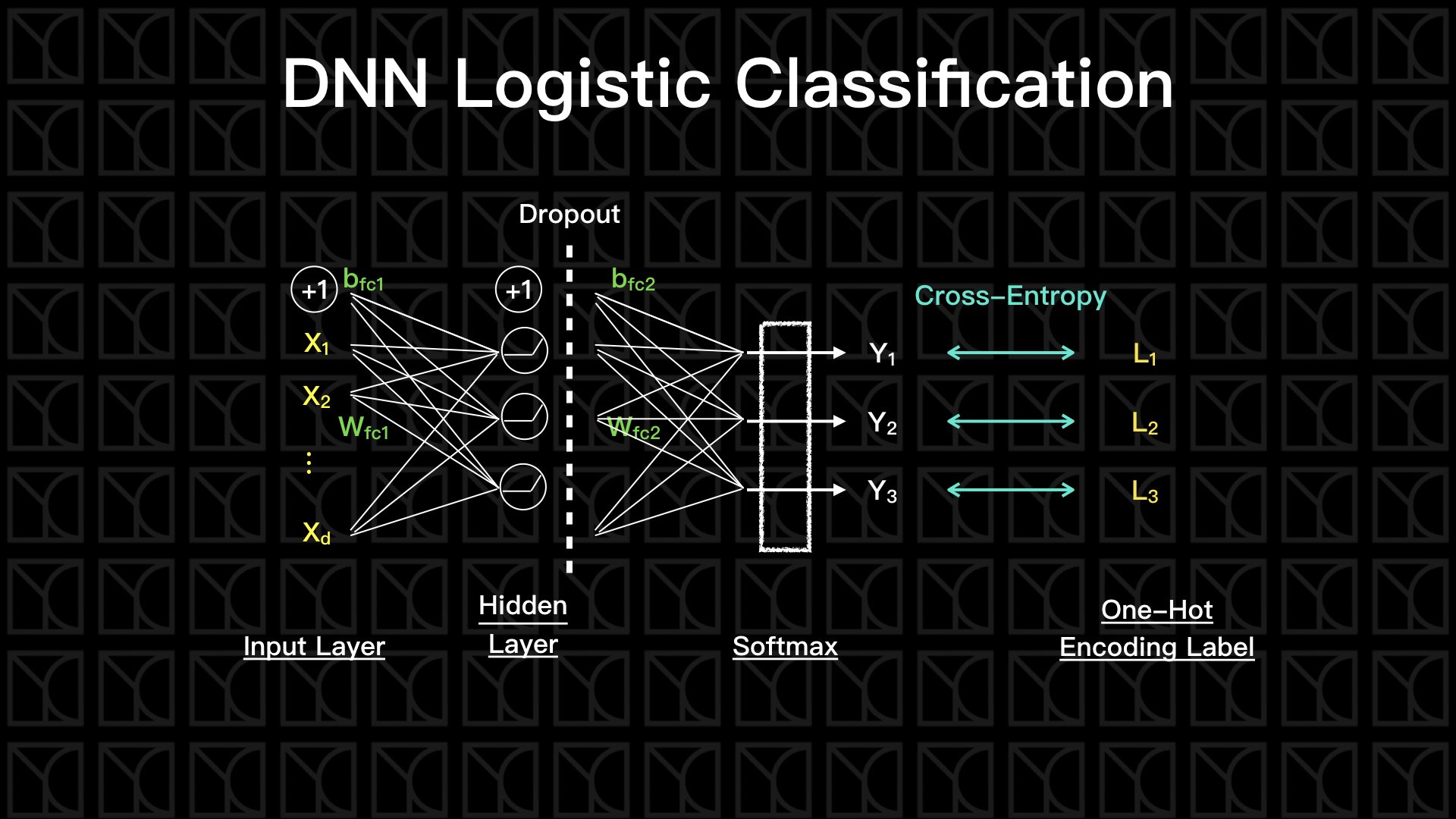
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155 | class DNNLogisticClassification:
def __init__(self, n_features, n_labels,
learning_rate=0.5, n_hidden=1000, activation=tf.nn.relu,
dropout_ratio=0.5, alpha=0.0):
self.n_features = n_features
self.n_labels = n_labels
self.weights = None
self.biases = None
self.graph = tf.Graph() # initialize new graph
self.build(learning_rate, n_hidden, activation,
dropout_ratio, alpha) # building graph
self.sess = tf.Session(graph=self.graph) # create session by the graph
def build(self, learning_rate, n_hidden, activation, dropout_ratio, alpha):
# Building Graph
with self.graph.as_default():
### Input
self.train_features = tf.placeholder(tf.float32, shape=(None, self.n_features))
self.train_labels = tf.placeholder(tf.int32, shape=(None, self.n_labels))
### Optimalization
# build neurel network structure and get their predictions and loss
self.y_, self.original_loss = self.structure(features=self.train_features,
labels=self.train_labels,
n_hidden=n_hidden,
activation=activation,
dropout_ratio=dropout_ratio,
train=True)
# regularization loss
self.regularization = \
tf.reduce_sum([tf.nn.l2_loss(w) for w in self.weights.values()]) \
/ tf.reduce_sum([tf.size(w, out_type=tf.float32) for w in self.weights.values()])
# total loss
self.loss = self.original_loss + alpha * self.regularization
# define training operation
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
self.train_op = optimizer.minimize(self.loss)
### Prediction
self.new_features = tf.placeholder(tf.float32, shape=(None, self.n_features))
self.new_labels = tf.placeholder(tf.int32, shape=(None, self.n_labels))
self.new_y_, self.new_original_loss = self.structure(features=self.new_features,
labels=self.new_labels,
n_hidden=n_hidden,
activation=activation)
self.new_loss = self.new_original_loss + alpha * self.regularization
### Initialization
self.init_op = tf.global_variables_initializer()
def structure(self, features, labels, n_hidden, activation, dropout_ratio=0, train=False):
# build neurel network structure and return their predictions and loss
### Variable
if (not self.weights) or (not self.biases):
self.weights = {
'fc1': tf.Variable(tf.truncated_normal(shape=(self.n_features, n_hidden))),
'fc2': tf.Variable(tf.truncated_normal(shape=(n_hidden, self.n_labels))),
}
self.biases = {
'fc1': tf.Variable(tf.zeros(shape=(n_hidden))),
'fc2': tf.Variable(tf.zeros(shape=(self.n_labels))),
}
### Structure
# layer 1
fc1 = self.get_dense_layer(features, self.weights['fc1'],
self.biases['fc1'], activation=activation)
if train:
fc1 = tf.nn.dropout(fc1, keep_prob=1-dropout_ratio)
# layer 2
logits = self.get_dense_layer(fc1, self.weights['fc2'], self.biases['fc2'])
y_ = tf.nn.softmax(logits)
loss = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=logits))
return (y_, loss)
def get_dense_layer(self, input_layer, weight, bias, activation=None):
# fully connected layer
x = tf.add(tf.matmul(input_layer, weight), bias)
if activation:
x = activation(x)
return x
def fit(self, X, y, epochs=10, validation_data=None, test_data=None, batch_size=None):
X = self._check_array(X)
y = self._check_array(y)
N = X.shape[0]
random.seed(9000)
if not batch_size:
batch_size = N
self.sess.run(self.init_op)
for epoch in range(epochs):
print('Epoch %2d/%2d: ' % (epoch+1, epochs))
# mini-batch gradient descent
index = [i for i in range(N)]
random.shuffle(index)
while len(index) > 0:
index_size = len(index)
batch_index = [index.pop() for _ in range(min(batch_size, index_size))]
feed_dict = {
self.train_features: X[batch_index, :],
self.train_labels: y[batch_index],
}
_, loss = self.sess.run([self.train_op, self.loss], feed_dict=feed_dict)
print('[%d/%d] loss = %9.4f ' % (N-len(index), N, loss), end='\r')
# evaluate at the end of this epoch
y_ = self.predict(X)
train_loss = self.evaluate(X, y)
train_acc = self.accuracy(y_, y)
msg = '[%d/%d] loss = %8.4f, acc = %3.2f%%' % (N, N, train_loss, train_acc*100)
if validation_data:
val_loss = self.evaluate(validation_data[0], validation_data[1])
val_acc = self.accuracy(self.predict(validation_data[0]), validation_data[1])
msg += ', val_loss = %8.4f, val_acc = %3.2f%%' % (val_loss, val_acc*100)
print(msg)
if test_data:
test_acc = self.accuracy(self.predict(test_data[0]), test_data[1])
print('test_acc = %3.2f%%' % (test_acc*100))
def accuracy(self, predictions, labels):
return (np.sum(np.argmax(predictions, 1) == np.argmax(labels, 1))/predictions.shape[0])
def predict(self, X):
X = self._check_array(X)
return self.sess.run(self.new_y_, feed_dict={self.new_features: X})
def evaluate(self, X, y):
X = self._check_array(X)
y = self._check_array(y)
return self.sess.run(self.new_loss, feed_dict={self.new_features: X,
self.new_labels: y})
def _check_array(self, ndarray):
ndarray = np.array(ndarray)
if len(ndarray.shape) == 1:
ndarray = np.reshape(ndarray, (1, ndarray.shape[0]))
return ndarray
|
| from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data/', one_hot=True)
train_data = mnist.train
valid_data = mnist.validation
test_data = mnist.test
|
| Extracting MNIST_data/train-images-idx3-ubyte.gz
Extracting MNIST_data/train-labels-idx1-ubyte.gz
Extracting MNIST_data/t10k-images-idx3-ubyte.gz
Extracting MNIST_data/t10k-labels-idx1-ubyte.gz
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | model = DNNLogisticClassification(
n_features=28*28,
n_labels=10,
learning_rate=0.5,
n_hidden=1000,
activation=tf.nn.relu,
dropout_ratio=0.5,
alpha=0.01,
)
model.fit(
X=train_data.images,
y=train_data.labels,
epochs=3,
validation_data=(valid_data.images, valid_data.labels),
test_data=(test_data.images, test_data.labels),
batch_size = 32,
)
|
| Epoch 1/ 3:
[55000/55000] loss = 0.4948, acc = 88.12%, val_loss = 0.5729, val_acc = 88.14%
Epoch 2/ 3:
[55000/55000] loss = 0.3343, acc = 91.21%, val_loss = 0.3831, val_acc = 91.04%
Epoch 3/ 3:
[55000/55000] loss = 0.2890, acc = 92.73%, val_loss = 0.3708, val_acc = 92.06%
test_acc = 91.17%
|
跟上次的結果比,你會發現有長足的進步,精確率來到90幾,大家可以下載程式碼,試著調整參數使得DNN Model的精確率可以更高,參數包含:
* Hidden Layer的神經元數量
* 不同的Activation Function
* 不同的Batch Size
* 調整Weight Regularization的比例
* 調整Dropout Ratio
* 選擇不同Optimizer
* 使得DNN更深
調整Model是重要的工作,試著自己動手做做看,你可以讓你的Model有多準呢?
