機器學習技法 學習筆記 (6)：神經網路(Neural Network)與深度學習(Deep Learning)

神經網路(Neural Network)

最後一個主題，我們要來講第三種「特徵轉換」— Extraction Models，其實就是現今很流行的「類神經網路」(Neural Network) 和「深度學習」(Deep Learning)，包括下圍棋的AlphaGo、Tesla的自動駕駛都是採用這一類的Machine Learning。

Extraction Models的基本款就是廣為人知的「神經網路」(Neural Network)，它的特色是使用神經元來做非線性的特徵轉換，那如果具有多層神經元，就是做了多次的非線性特徵轉換，這就是所謂的「深度學習」(Deep Learning)。

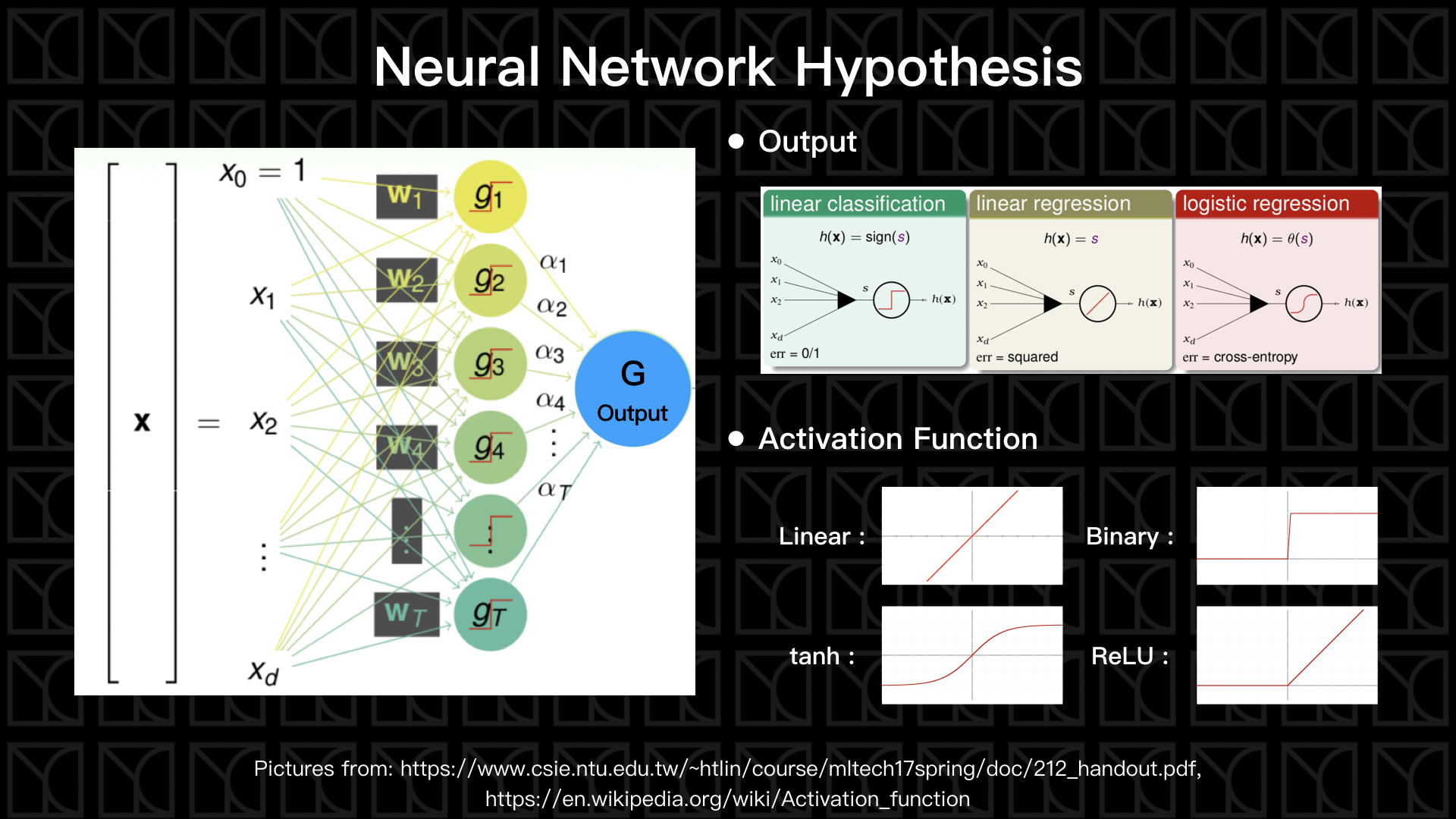
上圖左側就是具有一層神經元的Neural Network，首先我們有一組特徵\(X\)，通常我們會加入一個維度\(X_{0}=1\)，這是為了可以讓結構變得更好看，未來可以與\(W_{0}\)相乘產生常數項。使用\(W\)來給予特徵\(X\)權重，最後總和的結果稱之為Score，\(s = W_{0}X_{0}+𝚺_{i=1}W_{i}X_{i} = 𝚺_{i=0}W_{i}X_{i}\)。

這個Score會被輸入到一個Activation Function裡頭，Activation Function的用意就是開關，當Score大於某個閥值，就打通線路讓這條路的貢獻可以繼續向後傳遞；當Score小於某個閥值，就關閉線路，所以Activation Function可以是Binary Function，但在實際操作之下不會使用像Binary Function這類不可以微分的Activation Function，所以我們會找具有相似特性但又可以微分的函數，例如\(tanh\)或者是\(ReLU\)這類比較接近開關效果的函數，經過Activation Function轉換後的輸出表示成\(g_{t} = σ(𝚺_{i}W_{i}X_{i})\)，這個\(g_{t}\)就稱為神經元、\(σ\)為Activation Function、\(𝚺_{i} W_{i}X_{i}\)是Score。

如果我們有多組權重\(W\)就能產生多組神經元\(g_{t}\)，然後最後把\(g_{t}\)做線性組合並使用Output Function \(h(x)\)來衡量出最後的答案，Output Function可以是Linear Classification的Binary Function \(h(x)=sign(x)\)，不過一樣的問題，它不可以微分，通常不會被使用，常見的是使用Linear Regression \(h(x)=x\)，或者Logistic Regression \(h(x)=Θ(x)\)來當作Output Function，最後的結果可以表示成 \(y=h(𝚺_{t}α_{t}g_{t})\)，看到這個式子有沒有覺得很熟悉，它就像我們上一回講的Aggregation，將特徵X使用特徵轉換轉成使用\(g_{t}\)表示，再來組合這些\(g_{t}\)成為最後的Model，所以單層的Neural Network就使用到了Aggregation，它繼承了Aggregation的優點。

有了這個Model的形式了，我們可以使用Gradient Descent的手法來做最佳化，這也就是為什麼要讓操作過程當中所使用的函數都可以微分的原因。Gradient Descent在Neural Network的領域裡面發展出一套方法稱為Backpropagation，我們待會會介紹。因此實現Backpropagation，我只要餵Data進去，Model就會去尋找可以描述這組Data的特徵轉換\(g_{t}\)，這就好像是可以從Data中萃取出隱含的Feature一樣，所以這類的Models才會被統稱為Extraction Models。

深度學習(Deep Learning)

剛剛我們介紹了最基本款的Neural Network，那如果這個Neural Network有好幾層，我還會稱它為Deep Learning，所以基本上Deep Neural Network和Deep Learning是指同一件事，那為什麼會有兩個名字呢？其實是有歷史典故的。

Neural Network的歷史相當悠久，早在1958年就有人提出以Perceptron當作Activation Function的單層Neural Network，大家也知道一層的Neural Network是不Powerful的，所以在1969年，就有人寫了論文叫做「perceptron has limitation」，從那時起Neural Network的方法就很少人研究了。

直到1980年代，有人開始使用多層的Neural Network，並在1989年，Yann LeCun博士等人就已經將反向傳播演算法(Backpropagation, BP)應用於Neural Network，當時Neural Network的架構已經和現在的Deep Learning很接近了，不過礙於當時的硬體設備計算力不足，Neural Network無法發揮功效，並且緊接的有人在1989年證明了只要使用一層Neural Network就可以代表任意函數，那為何還要Deep呢？所以Deep Neural Network這方法就徹底黑掉了。

一直到了最近，G. E. Hinton博士為了讓Deep Neural Network起死回生，重新給了它一個新名字「Deep Learning」，再加上他在2006年提出的RBM初始化方法，這是一個非常複雜的方法，所以在學術界就造成了一股流行，雖然後來被證明RBM是沒有用的，不過卻因為很多人參與研究Deep Learning的關係，也找出了解決Deep Learning痛處的方法，2009年開始有人發現使用GPU可以大大的加速Deep Learning，從這一刻起，Deep Learning就開始流行起來，直到去年的2016年3月，圍棋程式Alpha GO運用Deep Learning技術以4:1擊敗世界頂尖棋手李世乭，Deep Learning正式掀起了AI的狂潮。

聽完這個故事我們知道改名字的重要性XDD，不過大家是否還有看到什麼關鍵，「使用一層Neural Network就可以代表任意函數，那為何還要Deep呢？」這句話，這不就否定了我們今天做的事情了嗎？的確，使用一層的Neural Network就可以形成任意函數，而且完全可以用一層的神經元來表示任何多層的神經元，數學上是行得通的，但重點是參數量。Deep Learning的學習方法和人有點類似，我們在學習一個艱深的理論時，會先單元式的針對幾個簡單的概念學習，然後在整合這些概念去理解更高層次的問題，Deep Learning透過多層結構學習，雖然第一層的神經元沒有很多，能學到的也只是簡單的概念而已，不過第二層再重組這些簡單概念，第三層再用更高層次的方法看問題，所以同樣的問題使用一層Neural Network可能需要很多神經元才有辦法描述，但是Deep Learning卻可以使用更少的神經元做到一樣的效果，

同樣表示的數學轉換過程，雖然單層和多層都是做得到相同轉換的，但是多層所用的參數量是比單層來得少的，依照VC Generalization Bound理論 (請參考：機器學習基石 學習筆記 (2)：為什麼機器可以學習?) 告訴我們可調控的參數量代表模型的複雜度，所以多層的NN比單層的有個優勢是在做到同樣的數學轉換的情況下更不容易Overfitting。

因此，Deep Learning中每一層當中做了Aggregation，在增加模型複雜度的同時，也因為平均的效果而做到截長補短，這具有Regularization的效果，並且在採用多層且瘦的結構也同時因為「模組化」而做到降低參數使用量，來減少模型複雜度，這就不難想像Deep Learning為何如此強大。

反向傳播算法(Backpropagation, BP)

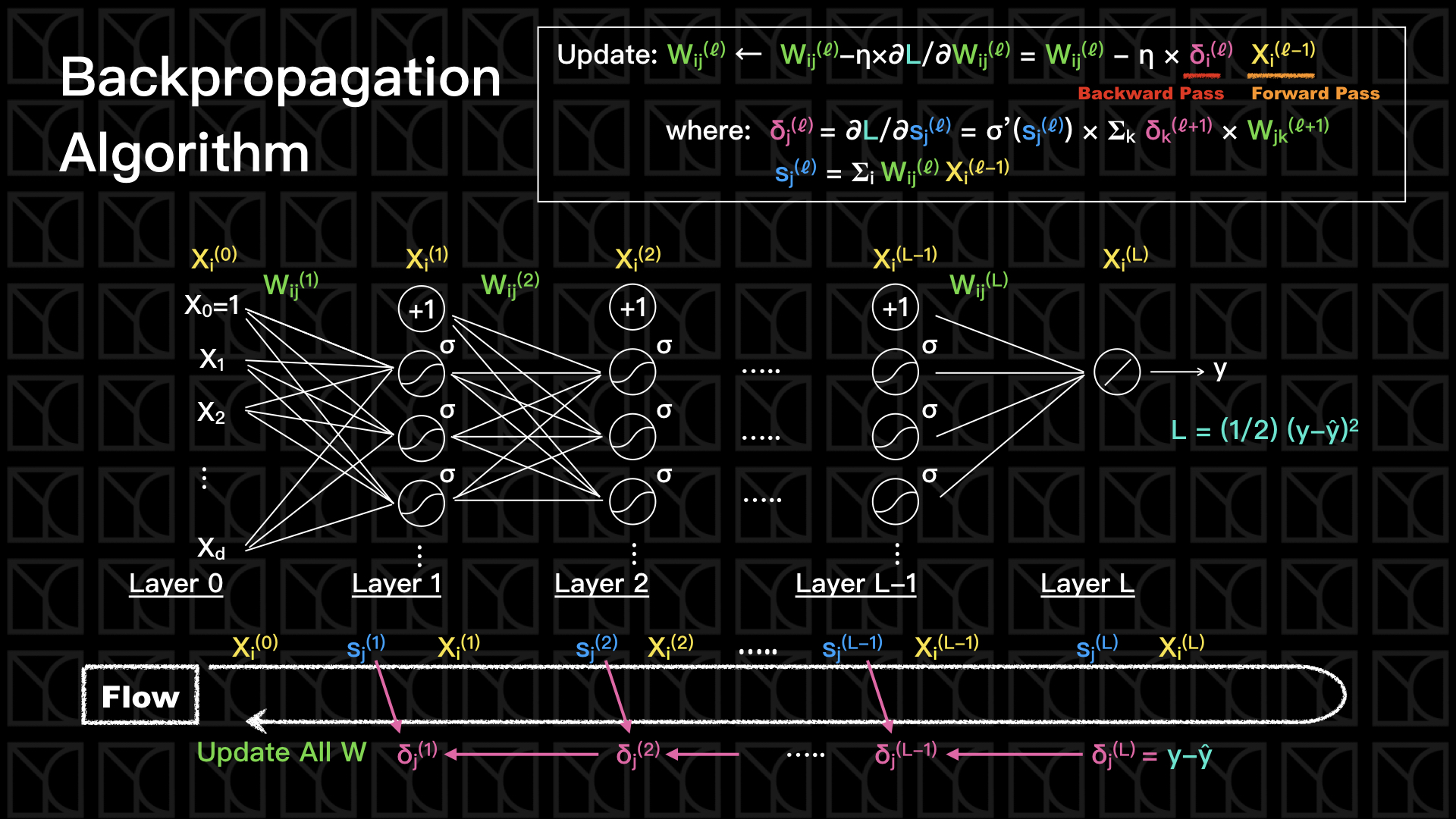
我們接下來就來看一下Deep Learning的演算法—反向傳播法，我們來看要怎麼從Gradient Descent來推出這個算法。

看一下上面的圖，我畫出了具有\(L\)層深的Deep Learning，每一層都有一個權重\(W_{ij}^{(ℓ)}\)，因此我們可以估計出每一層的Score \(s_{j}^{(ℓ)}= 𝚺_{i} W_{ij}^{(ℓ)}X_{i}^{(ℓ-1)}\)，把Score \(s_{j}^{(ℓ)}\)通過Activation Function，就可以得到下一層的Input，如此不斷的疊上去，直到最後一層L為Output Layer，Output最後的結果\(y\)，這裡我使用Linear Function來當作Output Function，這就是Deep Learning最簡單的架構。

而我們需要Training的就是這些權重\(W_{ij}^{(ℓ)}\)，我們如何一步一步的更新\(W_{ij}^{(ℓ)}\)，使得它可以Fit數據呢？回想一下Gradient Descent的流程：

1. 定義出Error函數
2. Error函數讓我們可以去評估\(E_{in}\)
3. 算出它的梯度\(∇E_{in}\)
4. 朝著\(∇E_{in}\)的反方向更新參數W，而每次只跨出\(η\)大小的一步
5. 反覆的計算新參數\(W\)的梯度，並一再的更新參數\(W\)

假設使用平方誤差的話，Error函數在這邊就是

\(L = (1/2) (y-\overline{y})^{2}\)，

因此我們的更新公式可以表示成

\(W_{ij}^{(ℓ)} ← W_{ij}^{(ℓ)}-η×∂L/∂W_{ij}^{(ℓ)}\)

那我們要怎麼解這個式子呢？關鍵就在\(∂L/∂W_{ij}^{(ℓ)}\)這項要怎麼計算，這一項在Output Layer (\(ℓ=L\))是很好計算的，

\(∂L/∂W_{ij}^{(L)}\)

\(= \frac{∂L}{∂s_{j}^{(L)}} \frac{∂s_{j}^{(L)}}{{∂W_{ij}^{(L)}}}\) (連鎖率)

\(= {δ_{j}^{(L)}}×{X_{i}^{(L-1)}}\)

上式當中我們使用了微分的連鎖率，並且令

\(δ_{j}^{(L)} = ∂L/∂s_{j}^{(L)}\)

\(δ_{j}^{(L)}\)這一項被稱為Backward Pass Term，而\(X_{i}^{(L-1)}\)這項被稱為Forward Pass Term，所以\(L\)層權重的更新取決於Forward Pass Term和Backward Pass Term相乘\(δ_{j}^{(L)}×X_{i}^{(L-1)}\)。

我們先來看一下\(L\)層的Forward Pass Term要怎麼計算，\(X_{i}^{(L-1)}\)這項是很容易求的，我們只要讓數據一路從\(0\)層傳遞上來就可以自然而然的得到\(X_{i}^{(L-1)}\)的值，所以我們會稱\(X_{i}^{(L-1)}\)這一項為Forward Pass Term，因為我們必須要往前傳遞才可以得到這個值。

再來看一下\(L\)層的Backward Pass Term要怎麼計算，\(δ_{j}^{(L)}\)一樣是很容易求得的，

\(δ_{j}^{(L)} = ∂L/∂s_{j}^{(L)} = ∂[(1/2) (y-\overline{y})^{2}]/∂y = (y-\overline{y})\)

你會發現這一項的計算需要得到誤差的資訊，而誤差資訊要等到Forward的動作做完才有辦法得到，所以資訊的傳遞方向是從尾巴一路回到頭，是一個Backword的動作。

因此，最後一層也是Output Layer的更新公式如下：

\(W_{ij}^{(L)} ← W_{ij}^{(L)}-η×δ_{j}^{(L)}×X_{i}^{(L-1)}\)

權重的更新取決於Input和Error的影響，需要考慮Forward Pass Term和Backward Pass Term。

那除了Output這一層以外的權重應該怎麼更新？來看一下\((ℓ)\)層，

\(∂L/∂W_{ij}^{(ℓ)}\)

\(= \frac{∂L}{∂s_{j}^{(ℓ)}}\frac{∂s_{j}^{(ℓ)}}{∂W_{ij}^{(ℓ)}}\) (連鎖率)

\(= δ_{j}^{(ℓ)}×X_{i}^{(ℓ-1)}\)

一樣是Forward Pass Term和Backword Pass Term相乘，不過\(δ_{j}^{(ℓ)}\)這一項的計算有點技巧性，來看一下，

\(δ_{j}^{(ℓ)}\)

\(= ∂L/∂s_{j}^{(ℓ)}\)

\(= 𝚺_{k} \frac{∂L}{∂s_{k}^{(ℓ+1)}}\frac{∂s_{k}^{(ℓ+1)}}{∂X_{jk}^{(ℓ)}}\frac{∂X_{jk}^{(ℓ)}}{∂s_{j}^{(ℓ)}}\) (連鎖率)

\(= 𝚺_{k} {δ_{k}^{(ℓ+1)}}×{W_{jk}^{(ℓ)}}×{σ'(s_{j}^{(ℓ)})}\)

\(W_{jk}^{(ℓ)}\)和\(σ'(s_{j}^{(ℓ)})\)都是Forward之後就會得到的資訊，而\(δ_{k}^{(ℓ+1)}\) 而是需要Backward才可以得到，我們已經知道\(δ_{j}^{(ℓ=L)}\)的值，就可以從\(δ_{j}^{(ℓ=L)}\)開始利用上面的公式，一路Backward把所有的\(δ_{j}\)都找齊。好！那現在我們已經找到了更新所有Weights的方法了。

看一下上圖中的最下面的Flow，一開始我們Forward，把所有\(X\)和\(s\)都得到，到了Output Layer，我們得到了\(δ_{j}^{(ℓ=L)}\)，再Backward回去找出所有的\(δ\)，接下來就可以用Forward Pass Term和Backword Pass Term來Update所有的\(W\)了。

總結一下，反向傳播算法(Backpropagation, BP)更新權重的方法為

\(W_{ij}^{(ℓ)} ← W_{ij}^{(ℓ)}-η×δ_{j}^{(ℓ)}×X_{i}^{(ℓ-1)}\)

If output layer (\(ℓ=L\)), \(δ_{j}^{(ℓ=L)}=(y-ŷ)\)

If other layer, \(δ_{j}^{(ℓ)}= σ'(s_{j}^{(ℓ)}) × 𝚺_{k} δ_{k}^{(ℓ+1)}×W_{jk}^{(ℓ)}\)

\(δ_{j}^{(ℓ)}\)為Backword Pass Term；\(X_{i}^{(ℓ-1)}\)為Forward Pass Term。

Regularization in Deep Learning

那麼使用Deep Learning的時候，我們要怎麼避免Overfitting呢？有五個方法。

第一個方法，就是我們剛剛提過的「設計Deep Neural Network的結構」，藉由限縮一層當中的神經元來達到一種限制，做到Regularization。

第二個方法是「限制W的大小」，和標準Regularization作一樣的事情，我們將\(W\)的大小加進去Cost裡頭做Fitting，例如使用L2 Regularizer \(Ω(W)=𝚺(W_{jk}^{(ℓ)})^{2}\)，但這樣使用有一個問題就是\(W\)並不是Sparse的，L2 Regularizer在抑制\(W\)的方法是，如果W的分量大的話就抑制多一點，如果分量小就抑制少一點（因為\(W^{2}\)微分為1次），所以最後會留下很多很小的分量，造成計算量大大增加，尤其像是Deep Learing這麼龐大的Model，這樣的Regularization顯然不夠好，L1 Regularizer顯然可以解決這個問題（因為在大部分位置微分為常數），但不幸的是它無法微分，所以就有了L2 Regularizer的衍生版本，

Weight-elimination L2 regularizer: \(𝚺\frac{(W_{jk}^{(ℓ)})^{2}}{1+(W_{jk}^{(ℓ)})^{2}}\)

這麼一來不管\(W\)大或小，它受到抑制的值大小是接近的 (因為Weight-elimination L2 regularizer微分為 \(-1\)次方)，因此就可以使得部分\(W\)可以為\(0\)，大大便利於我們做計算。

第三種方法是最常使用的「Early Stopping」，所謂的Early Stopping就是，在做Backpropagation的過程去觀察Validation Data的Error有沒有脫離Training Data的Error太多，如果開始出現差異，我們就立刻停止計算，這樣就可以確保Model裡的參數沒有使得Model產生Overfitting，是一個很直接的作法。

第四種方法是「Drop-out」，在Deep Learing Fitting的過程中，隨機的關閉部分神經元，藉由這樣的作法使得Fitting的過程使用較少的神經元，並且使得結構是瘦長狀的，來達到Regularization。

第五種方法是接下來會用更大篇幅介紹的「Denoising Autoencoder」，在Deep Neural Network前面加入這樣的結構有助於抑制雜訊。

Autoencoder

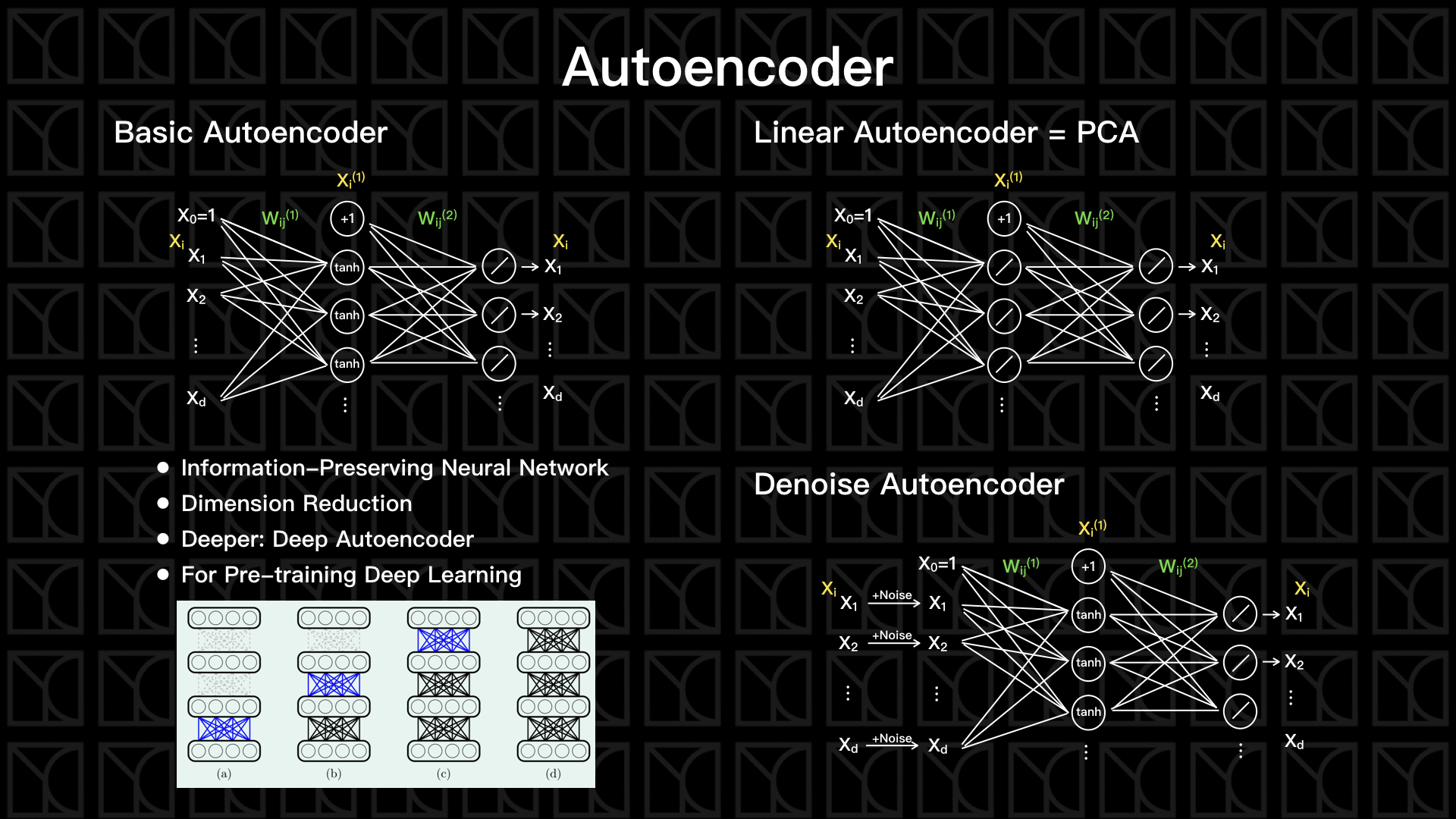
Neural Network針對不同需要發展出很多不同的型態，包括CNN, RNN，還有接下來要介紹的Autoencoder，Autoencoder是一種可以將資料重要資訊保留下來的Neural Network，效果有點像是資料壓縮，在做資料壓縮時，會有一個稱為Encoder的方法可以將資料壓縮，那當然還要有另外一個方法將它還原回去，這方法稱為Decoder，壓縮的過程就是用更精簡的方式保存了資料。Autoencoder同樣的有Encoder和Decoder，不過它不像資料壓縮一樣可以百分之一百還原，不過特別之處是Autoencoder會試著從Data中自己學習出Encoder和Decoder，並盡量讓資料在壓縮完了可以還原回去原始數據。

見上圖中Basic Autoencoder的部分，透過兩層的轉換，我們試著讓Input \(X\)可以完整還原回去，通常中間這一層會使用比較少的神經元，因為我們想要將資訊做壓縮，所以第一層的部分就是一個Encoder，而第二層則是Decoder，他們由權重\(W_{jk}^{(ℓ)}\)決定，而在Training的過程，Autoencoder會試著找出最好的\(W_{jk}^{(ℓ)}\)來使得資訊可以盡量完整還原回去，這也代表Autoencoder可以自行找出了Encoder和Decoder。

Encoder這一段就是在做一個Demension Reduction，Encoder轉換原本數據到一個新的空間，這個空間可以比原本Features描述的空間更能精準的描述這群數據，而中間這層Layer的數值就是新空間裡頭的座標，有些時候我們會用這個新空間來判斷每筆Data之間彼此的接近程度。

我們也可以讓Encoder和Decoder可以設計的更複雜一點，所以你同樣的可以使用多層結構，稱之為Deep Autoencoder。另外，也有人使用Autoencoder的方法來Pre-train Deep Neural Network的各個權重。

緊接著介紹兩種特殊的例子，第一個是Linear Autoencoder，我們把所有的Activation Function改成線性的，這個方法可以等效於待會要講的Principal Component Analysis (PCA)的方法，PCA是一個全然線性的方法，所以它的效力會比Autoencoder差一點。

第二個是剛剛提到的Denoising Autoencoder，我們在原本Autoencoder的前面加了一道增加人工雜訊的流程，但是又要讓Autoencoder試著去還原出原來沒有加入雜訊的資訊，這麼一來我們將可以找到一個Autoencoder是可以消除雜訊的，把這個Denoising Autoencoder加到正常Neural Network的前面，那這個Neural Network就擁有了抑制雜訊的功用，所以可以當作一種Regularization的方法。

Principal Component Analysis (PCA)

最後來講一下Principal Component Analysis (PCA)，它不太算是Deep Learning的範疇，不過它是一個傳統且重要的Dimension Reduction的方法，我們就來看一下。

PCA的演算法是這樣的，第一步先求出資料Features的平均值，並且將各個Features減掉平均值，令為\(ζ\)，第二步求出由\(ζ^{T}ζ\)產生的矩陣的Eigenvalue和Eigenvector，第三步，從這些Eigenvalue和Eigenvector中挑選前面\(k\)個，並組成轉換矩陣\(W\)，而最終PCA的轉換就是\(Φ(x)=W^{T}(X-mean(X))\)，這個轉換做的就是Dimension Reduction，將數據降維到\(k\)維。

PCA做的事是這樣的，每一個Eigenvector代表新空間裡頭的一個軸，而Eigenvalue代表站在這個軸上看資料的離散程度，當然我們如果可以描述每筆資料越分離，就代表這樣的描述方法越好，所以Eigenvalue越大的Eigenvector越是重要，所以取前面\(k\)個Eigenvector的用意是在降低維度的過程，還可以盡量的保持對數據的描述力，而且Eigenvector彼此是正交的，也就是說在新空間裡頭的每個軸是彼此垂直，彼此沒有Dependent的軸是最精簡的，所以PCA所做的Dimension Reduction一定是線性模型中最好、最有效率的。

另外，剛剛有提到的Linear Autoencode幾乎是等效於PCA，大家可以看上圖中的描述，這裡不多贅述，不過不同的是，Linear Autoencoder並沒有限制新空間軸必須是正交的特性，所以它的效率一定會比PCA來的差。

結語

這一篇當中，我們介紹了Neural Network，並且探討多層Neural Network—Deep Neural Network，也等同於Deep Learning，並且說明為什麼需要「Deep」，然後介紹Deep Learning最重要的演算法—反向傳播算法，接著介紹五種常用的Regularization的方法：設計Deep Neural Network的結構、限制W的大小、Early Stopping、Drop-out和Denoising Autoencoder。

介紹完以上內容，我們就已經對於Deep Learning的全貌有了一些認識了，緊接著來看Deep Learning的特殊例子—Autoencoder，Autoencoder可以用來做Dimension Reduction，那既然提到了Dimension Reduction，那就不得不在講一下重要的線性方法PCA。

那在下一回，我們會繼續探討Neural Network還有哪些特殊的分支。