機器學習基石學習筆記 (2)：為什麼機器可以學習?

Posted on June 26, 2016 in AI.ML. View: 12,246

前言

在上一回當中，我們初探了機器學習，了解了什麼時候適合使用機器學習，而不是一般的Hard Coding，那今天這篇文章要繼續問下去。

為什麼機器可以學習(Why Can Machines Learn?)，本篇會介紹學理上機器學習（ML）必須要有哪些條件才可行，這些理論有非常多的數學，但卻是了解機器學習非常重要的內功，我會盡量避開繁複的數學運算，而帶大家直接的了解式子所要告訴我們的觀念。

機器可以學習嗎?

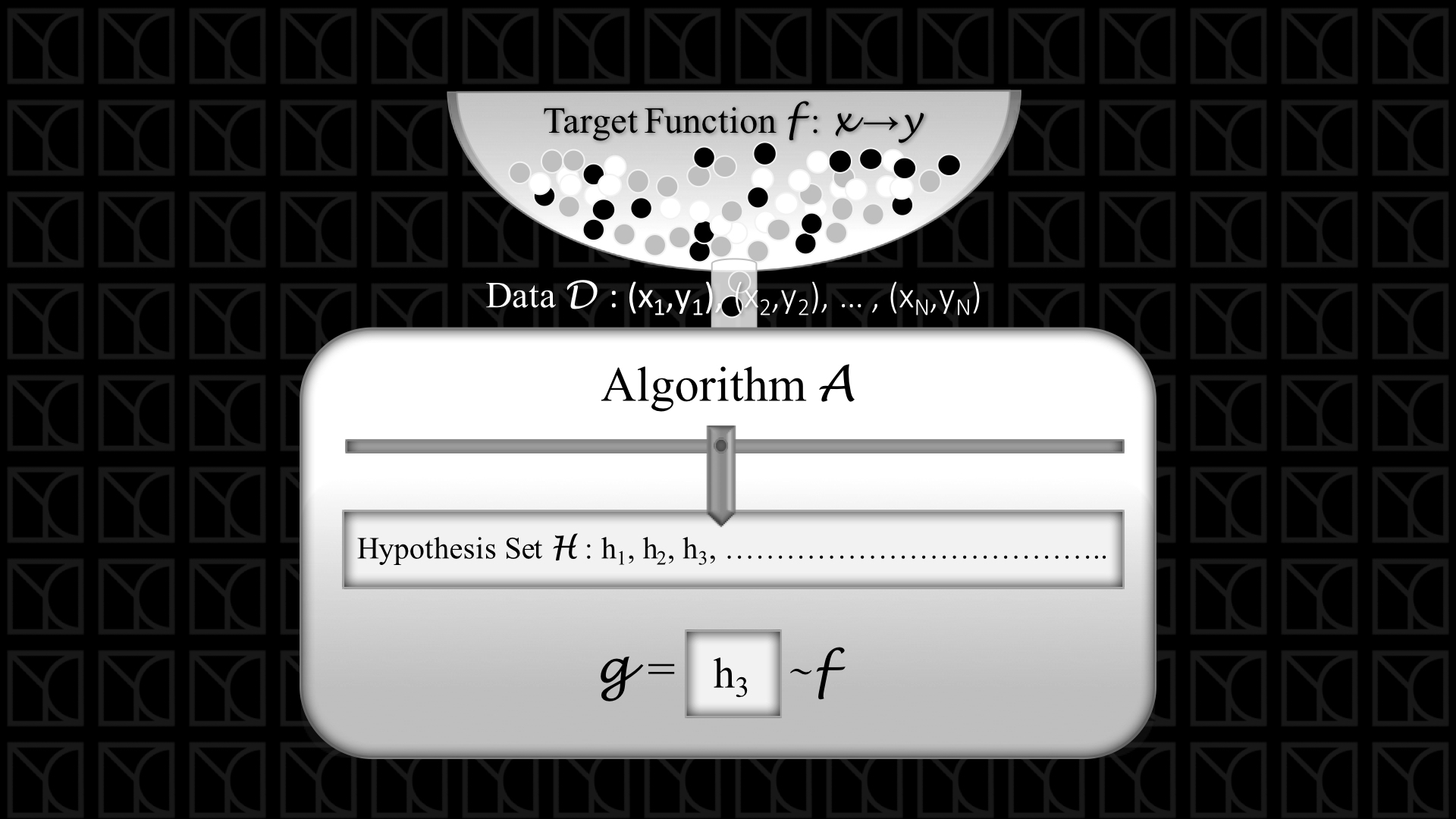
MachineLearningFoundations.001

還記得上面這張圖嗎? 上次帶大家初探了Machine Learning(ML)的基本架構，可以把整個概念總結成上面這張圖。

我們來複習一下，先從最上面的盆子開始看起，我們用Target Function代表你想要學習的技能，在非常理想的情況下，也就是沒有noise的情況，每組輸入變數 $X_n$都會找到一組精確的輸出 $y_n$，而這個Target Function能產生多個Data，圖中那些小球就是代表由Target Function產生的Data，今天我從中隨機抽取出$N$組Data來做機器學習，接下來Learning Algorithm會利用這些取出的Data去找出最吻合的Hypothesis，那這組Hypothesis就成了我們學習出來的結果，我們可以利用這個結果來預測新的問題。

那麼上面這張圖真的合理嗎? 我們真的有辦法用上面的方法讓機器學習嗎?

先介紹幾個名詞，我們會稱抽樣的Data為In-sample Data，並且稱Hypothesis預測In-sample Data的誤差為In-sample Error，記作$E_{in}$，因此Learning Algorithm的目的就是找出那組Hypothesis使得$E_{in}$最小。

回想一下二元分類問題，在上一篇當中我們使用PLA來挑選Hypothesis Set，還記得我們做了什麼事來確保我們可以得到最佳解嗎? 那就是Pocket的方法，Pocket的目的就是去留住一組能預測最好的Hypothesis，也就是能保留一組最佳參數使得$E_{in}$最小。

但如果$E_{in}$真的已經可以壓到0了，我們就可以說機器學習已經完成了嗎？

並不是這樣的，回到目的，我們真正希望的是機器有辦法預測新的問題，所以真正的目標是能將「沒有看過的Data」也可以預測好，而不是單單將取樣的Data預測好就夠了。

我們會稱未被取樣的Data為Out-of-sample Data，並且稱Hypothesis預測Out-of-sample Data的誤差為Out-of-sample Error，記作$E_{out}$，我們最終目的就是把$E_{out}$壓下來，也就代表可以預測新的問題。

但遺憾的是我們不會真正知道$E_{out}$，除非我們知道Target Function，所以我們只能評估$E_{in}$來選取Model參數，因此重要的是需要$E_{in} \approx E_{out}$這個條件要成立，否則一切的學習都是無效的。

總結一下機器學習的條件，我們必須建立一個 Learning Model可以確保$E_{in}\approx E_{out}$，所以在Learning Algorithm選出最小$E_{in}$的Hypothesis，同時這組Hypothesis也可以很好的預測Out-sample，我們就可以說機器已經會學習了。

$E_{in}$和$E_{out}$的差異

剛剛我們已經提到了如果機器能學習，那就必須先確保$E_{in} \approx E_{out}$，下面我會引入Hoeffding不等式來說明這個條件怎麼成立。

先想像一下我有一個桶子，這個桶子裝了兩種顏色的小球，分別為橘色和綠色，今天如果桶子內橘色球佔的比例為$μ$，而今天我們從中隨機抽樣出$N$顆小球，並且計算出這$N$顆小球中橘色佔的比例為$ν$，此時我們可以想像的到，$μ=ν$不一定會成立，但$μ$也不至於離$ν$太遠，所以Hoeffding不等式就告訴我們$|μ-ν|$會被限制在一個範圍內，表示為：

$$ \mathbb{P}[|ν-μ|>ε] \leq 2 exp(-2ε^2N) $$

當$ε$越大，出現的機率就越低。

接下來我們再把橘球和綠球的意義換成是，一組Hypothesis預測每筆Data的好或壞，預測正確的是綠球，預測失敗的是橘球，所以對於In-Sample來說，$μ$ 就是 $E_{in}$

$$ μ = (1/N) \sum_{n=1}^N ⟦h(x)\neq y_n⟧ = E_{in}(h) $$

對於Out-Sample來說，$ν$ 就是 $E_{out}$

$$ ν = ε_{x \sim P} ⟦h(x)\neq f(x)⟧ = E_{out}(h) $$

套入剛剛的不等式，得

$$ \mathbb{P}[|E_{in}(h)-E_{out}(h)|>ε] \leq 2 exp(-2ε^2N) $$

上面這個式子告訴我們$E_{in}$和$E_{out}$差距超過$ε$的可能性是被限制住的，只要抽樣的數量$N$夠多，基本上$E_{in}\approx E_{out}$就成立，我們這邊定義那些超出$ε$的Data為Bad Data(不好的數據)，Bad Data出現的可能是被Bound住的，所以機器學習是有可能的。

而事實上，我們的hypothesis不會只有一個，所以接下來來考慮如果有M個Hypotheses的情況下我們的$E_{in}$和$E_{out}$的差異會怎麼被參數影響。

如果我們考慮M組Hypotheses，就會發現每種Hypothesis出現Bad Data的地方可能不一樣，因此大大的減少能使用的Data，如上圖左側所示。

今天如果我有1000份從Target Function取$N$個Data的情形，然後只用一個Hypothesis來衡量，根據Hoeffding's Inequality，1000份裡面假設大概5份會出現Bad Data，但今天我再增加一組Hypothesis來衡量，對於這個Hypothesis也可能有自己的5份Bad Data，如果很不幸的，剛剛好這5份Bad Data和前5份沒有重疊，因此用這兩個hypotheses來評估的話，1000份裡頭將會出現10份的Bad Data，由此類推，如果有$M$組Hypotheses，最差的情況會發生在什麼時候呢? 那就是$M$個Hypotheses的每份Bad Data彼此都沒有交集，夠慘吧! 所以把這些出現Bad Data的機率取聯集得到以下式子：

$$ \mathbb{P}[\exists h\in \mathbb{H}\ s.t.\ |E_{in}(h)-E_{out}(h)|>ε] \leq 2M exp(-2ε^2N) $$

大家現在回想一下上一篇所提到的Perceptron Hypothesis Set就會發現，糟糕了! Perceptron Hypothesis Set 裡有無限多組的Hypotheses，也就是$M→∞$，那我們不就需要無限多的Data才能做到$E_{in} \approx E_{out}$，否則機器根本不會學習，所以前一篇的內容都在亂講，PLA根本無法學習，因為$E_{in} \approx E_{out}$，就算$E_{in}$很小也不代表學習成立，機器學習是不可能的。等一下！先沉住氣，聽我接下來慢慢解釋，你就會發現還有一線生機。

VC Generalization Bound

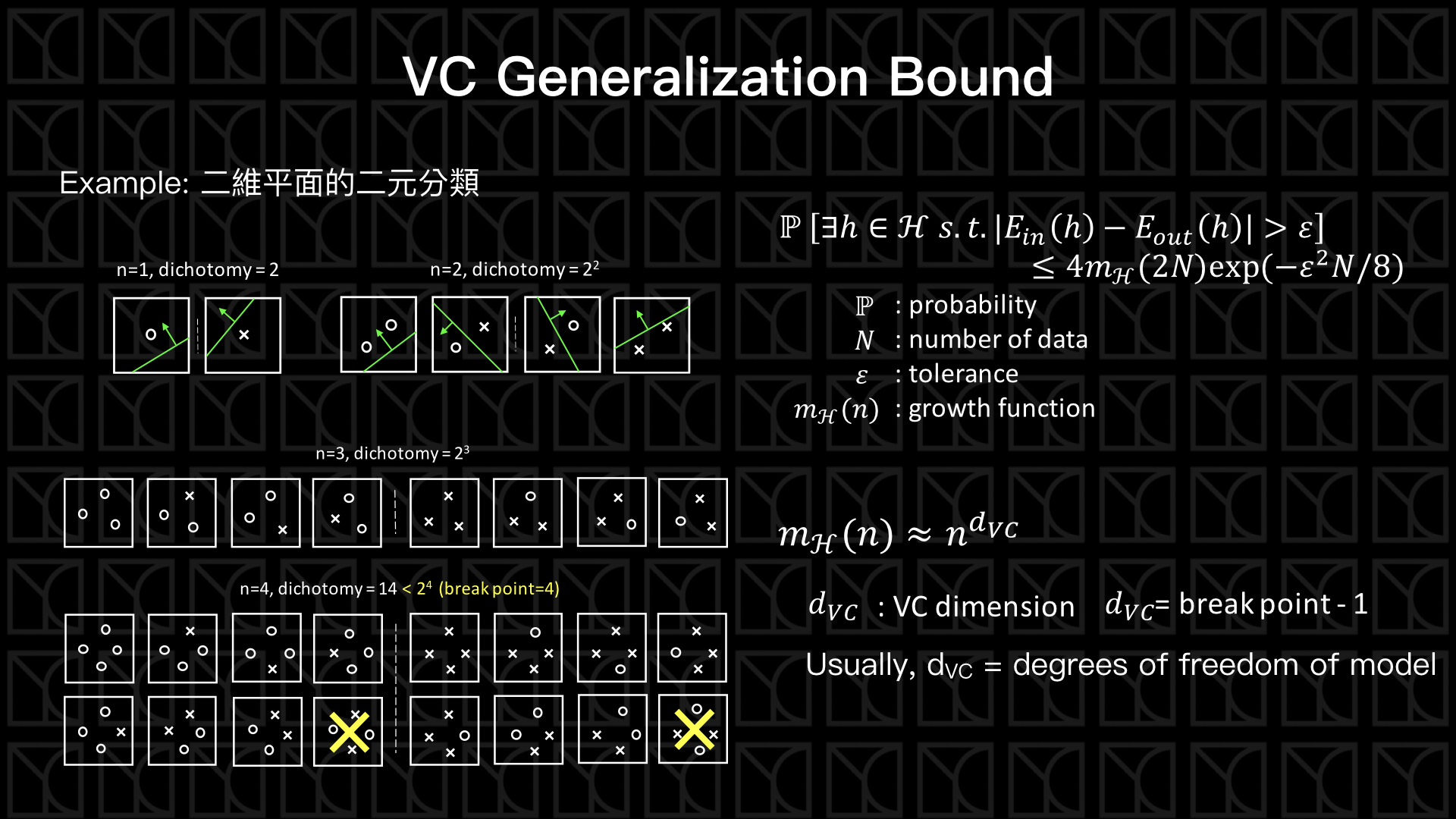
問題出在這裡，我們在Multi-Bin Hoeffding’s Inequality中採用了一個假設，就是假設每組Hypotheses的Bad Data彼此間都沒有重疊，所以在$M→∞$的情況下，當然會有一個無限大的上限值，但如果考慮了Bad Data重疊的情形，縱使$M→∞$的情況下還是有機會把Bad Data的出現機率壓在一個有限的定值之下。

我們回到二元分類問題，看一下上圖中左側的圖例，如果今天在二維平面上做二元分類，當數據量只有1個$n=1$時，就算你的切法有無窮多種，但對於一組Data來說就只有兩類Hypotheses而已，再來看$n=2$的情況，一樣的無限多組的切法但Hypotheses也只能歸類成4類。

所以Hypotheses用來描述數據的情況是彼此有所重疊的，也就是Bad Data出現的情形在許多Hypotheses是相同的。

但是聰明的你一定想到，如果今天$n$的數量不斷的增加，則Hypotheses被分類的數量就會成指數 $2^n$ 增加，Hypotheses彼此之間Bad Data的重疊情況就會漸漸減少，因此仍然無法限制住Bad Data的數量。

先別緊張，我們繼續看下去，當$n=3$，沒有意外的Hypotheses會被分類為8類，那接下來$n=4$時，你就會發現一個有趣的現象，開始有一些分類情況是不會出現的，因為它無法被一分為二，因此我們擔心因為Data數量增加而造成Hypotheses的種類暴增的情形被排除了，有一些狀況是不會出現的，Hypotheses是有重疊的。

剛剛所提到的分類方式的數量稱為Dichotomy。在$n=1$、$n=2$到$n=3$的情形，所有列得出來的方式都可被完整分類開來，我們稱這情形為Shatter，但是到了$n=4$的時候，有些不可能被分類的情形出現了，稱為不可被Shatter，另外我們又稱此情形開始發生的那點為Break Point，這邊注意一下喔! 會不會存有Break Point取決於你的Hypothesis Set長怎麼樣，現在這個例子的Break Point在$n=4$，其他的Hypothesis Set就不一定了。

Break Point的出現非常重要，他所代表的是Bad Data的出現機率不會無所限制的大下去，因此把這概念帶入Multi-Bin Hoeffding’s Inequality，經過繁複的計算，就可以得到以下公式：

$$ \mathbb{P}[\exists h\in \mathbb{H}\ s.t.\ |E_{in}(h)-E_{out}(h)|>ε] \leq 4m_{\mathbb{H}}(2N) exp(-ε^2N/8) $$

，原本的$M$消失了，取而代之的是Growth Function $m_{\mathbb{H}}(2N)$，Growth Function與Data數量$N$有關，這就是我們剛剛解說的，決定Hypothesis Set的種類的其實是 Data的數量$N$。

那麼Growth Function要怎麼和Break Point連結起來呢？

先定義一下VC Dimension：$d_{VC}= Break Point-1$，Break Point代表首次出現不Shatter的情況，那比它小一級代表的正是最大可以Shatter的點，上面的例子中$d_{VC}=3$。而這個VC Dimension就可以和我們在意的Growth Function連接起來，經過數學推倒可以得到以下關係式：

$$ m_{\mathbb{H}}(n) = n^{d_{VC}},\ d_{VC} = BreakPoint-1 $$

所以我們就知道啦！只要有Break Point存在，VC Dimension就是一個有限的值，也因此Growth Function是一個有限的值，VC Bound就產生了，就可以確保Bad Data出現的機率被壓在一個定值之下，所以一樣的只要資料量$N$夠多就可以確保$E_{in} \approx E_{out}$，機器將可以學習。

另外一件重要的事，VC Dimension在數學上是有意義的，$d_{VC} \approx 可調控變數的個數$，像是上述的二維二元分類問題，它的可調控變數有$w_0$, $w_1$ 和 $w_2$，總共3個，所以$d_{VC}=3$。也就是說Hypothesis Set的可調變參數如果是有限，大部分都可以做機器學習。

機器要能學習的三要素

前面拉哩拉雜的講了一堆，終於要推出我們的結論了! 所以如果剛剛的數學讓你感到很挫敗，沒關係，讀懂這段那就足夠了。

從VC Generalization Bound，我們可以知道機器學習是可能的，只要它具備三點要素：

Good Hypothesis Set: Hypothesis Set 必須有Break Point的存在，也意味著VC Dimension是有限的，而且越小越好，在意義上代表可以調控的變數不要太多。
Good Data: 數據量越大越好，可以壓低VC Generalization Bound
Good Learning Algorithm: 以上兩點可以確定的是$E_{in} \approx E_{out}$，接下來好的Learning Algorithm要有能力找到$E_{in}$ 最小的參數。很直觀的，當我們可以調控的變數越多，我們的選擇就越多，也就是我們可以找到更小$E_{in}$ 的機會變多了，所以可以調控的變數不可以太少。

眼尖的你有沒有發現矛盾啊! 可以調控的變數很少，我們能確保$E_{in} \approx E_{out}$，但是如果我想要找到更小的$E_{in}$ 又必須有更多的調控變數，這個矛盾是機器學習上一個重要的課題，解法是我們必須要能找到適當的調控變數數量，也就是適當大小的$d_{VC}$ 。

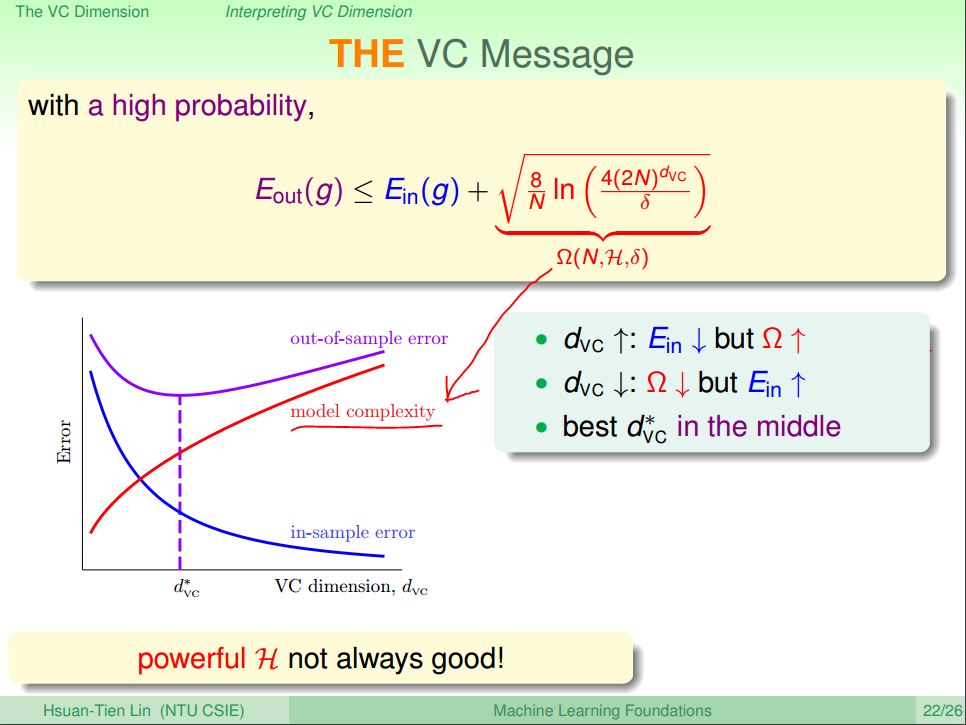
from: https://d396qusza40orc.cloudfront.net/ntumlone/lecture_slides/07_handout.pdf

上圖中，我們把VC Generalization Bound公式帶入Growth Function和$d_{VC}$的關係式，並且設$δ$ 為最大可以容忍的Bad Data出現機率，把它帶入取代掉$ε$，整理一下，就可以推出上圖的公式，$\Omega (N,\mathbb{H},δ)$稱為Model Complexity，這一項代表的是Hypothesis Set的大小造成的模型複雜度，它隨著$d_{VC}$增加而增加。Model Complexity越大代表Bad Data更容易出現，所以$E_{in}$和$E_{out}$開始被帶開了。

這個現象有一個很常見的名字叫做Overfitting，指的是使用非常複雜的Model來Fitting，雖然可以把手頭上的數據Fit的很漂亮，但是拿到其他的數據來看就會發現這Model的預測性非常的差，原因就是因為Model Complexity造成$E_{in}$和$E_{out}$脫鉤了，所以選擇一個複雜度適中的Model是很重要的。

機器學習架構一般化

最後我們來總結一下機器學習的流程，上圖中是之前提到的機器學習的架構並額外考慮一些真實情形，

每筆Data出現的機會不一定，同樣的採樣結果也是會受機率的影響，所以上圖中標示為$\mathbb{P} (x)$，這個修改並不會影響機器學習的流程和結果。
Data可能會受到Noise的影響，所以給定$X_n$並不一定會百分之一百得到$y_n$，他存在著可能會出錯，上圖標示為$\mathbb{P}(y|x)$，我們可以增大我們採樣的數量$N$來減少Noise的影響。
我們是採用$E_{in}$來當作選擇Model參數的指標，因此我們需要訂出Error的評估方式，常見的有Squared Error $E_{squared} = (y_n - y_{prediction})^2$。

跟著架構我們就有一套機器學習的標準流程，

準備好足夠的數據
把Model建立好，$d_{VC}$必須要是有限的，而且大小要適中
定義好評估$E_{in}$的Error Measurement
使用演算法找出最佳參數把$E_{in}$降低
最後評估一下是否有Overfitting的狀況，確保$E_{in} \approx E_{out}$（未來會講怎麼做）

Previous Post Next Post

前言

機器可以學習嗎?

\(E_{in}\)和\(E_{out}\)的差異

VC Generalization Bound

機器要能學習的三要素

機器學習架構一般化

You might enjoy