機器學習技法 學習筆記 (7):Radial Basis Function Network與Matrix Factorization
Posted on April 22, 2017 in AI.ML. View: 16,072
Radial Basis Function (RBF) Network
回顧一下Gaussian Kernel SVM,
\(W = 𝚺_{n=sv} α_n y_n Z_n\)
\(G_{SVM}\)
\(= sign[WZ+b]\)
\(= sign{[𝚺_{n=sv} α_n y_n K(X_n,X)]+b}\)
\(⇒ G_{SVM} = sign{[𝚺_{n=sv} α_n y_n exp(-γ |X-X_n|^2)]+b}\)
看到這個式子你想到了什麼?有沒有融會貫通的感覺,你同樣的可以把上面的式子看成是Aggregation,又或者是Network。
先來定義一下RBF Function, 其實就是Gaussian Function,
RBF Function: \(RBF(X,X_n)=exp(-γ|X-X_n|^2)\)
所以我們可以仿造SVM的形式來造一個Network,
\(G=Output{[𝚺_m β_m RBF(X,μ_m)]+b}\)
當\(Output\)為\(sign\) Function、\(β_m\)為\(α_n y_n\)就回到特例SVM了。
我們來細看這個式子傳遞的概念,RBF Network的第一層是先產生\(M\)組\(RBF(X,μ_m)\),意味著以這\(M\)個位置\(μ_m\)當作中心點來評估各個\(X\)與它的相似程度,RBF是有評估相似度的味道,越接近\(μ_m\)的點,RBF越大,並隨著與\(μ_m\)距離變大,RBF的值也快速遞減,所以這\(M\)個\(μ_m\)是有象徵性的,越接近它你越受它的影響。
決定了每一筆數據各是受哪些\(μ_m\)影響,接下來第二層是由這M個代表性的位置來進行投票決定最後的結果,這意味的不同的地方對\(μ_m\)最後結果也有不同的影響力,舉個例子,假設在SVM裡頭,某個\(μ_m\)如果它的\(y_m =+1\),那它對最後的影響就會是正的;那如果某個\(μ_m\)的\(y_m=-1\),那它對最後的影響就會是負的,所以一個點進來,先評估一下它和象徵性的幾個點\(μ_m\)的距離,如果相鄰幾點都是正的,這個點最後的結果就會是正的。
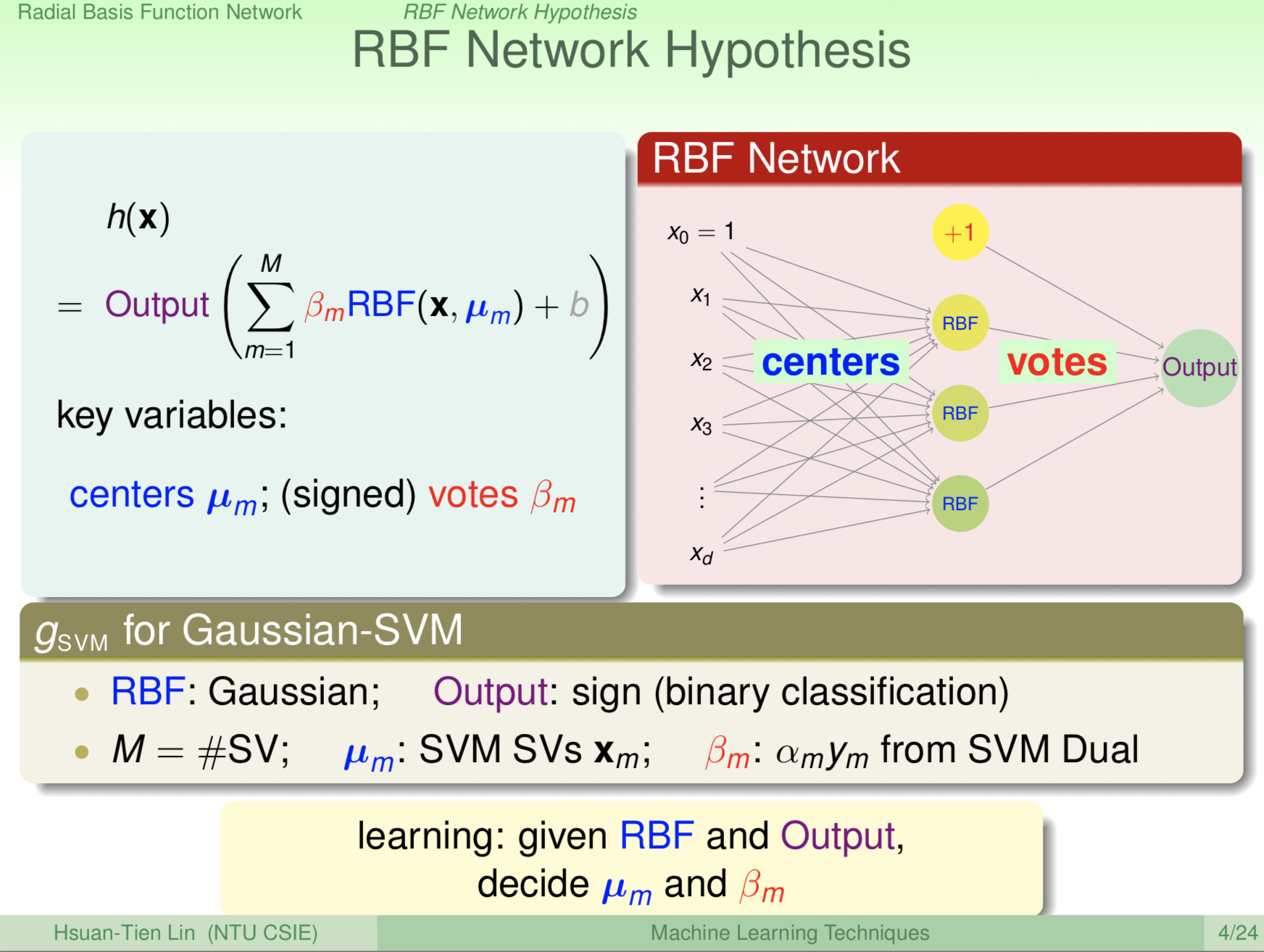
From: https://www.csie.ntu.edu.tw/~htlin/course/mltech17spring/doc/214_handout.pdf
RBF Network在歷史上是Neural Network的一個分支,不過從上面的介紹你就會發現,它們的結構是有差異的,演算法也就不一樣。
通常最佳化RBF Network做法是這樣的,我們會先用一些方法將\(μ_m\)決定,如果\(μ_m\)很懶惰的就直接使用所有的Training Data,總共有\(N\)個,這\(μ_m\)就叫做「Full RBF Network」。我們也可以使用一些歸納的演算法找出代表資料群體的幾個象徵性的中心點,例如待會會介紹的K-Means的方法,找出k個\(μ_m\)再做計算,這樣的RBF Network稱為「k Nearest Neighbor RBF Network」。
找到了\(μ_m\)就已經決定了所有的RBF Function,接下來就可以線性組合這些RBF Function,我們可以使用Regression的方法來求取\(β_m\)。
而如果你使用「Full RBF Network」,你會發現做完Regression後\(E_{in}=0\),這是典型的Overfitting,那這時你可能就要採用有Regularization的Regression啦!譬如說Ridge Regression之類的。
K-Means

From: https://www.csie.ntu.edu.tw/~htlin/course/mltech17spring/doc/214_handout.pdf
接下來來看怎麼用K-Means找到代表資料群體的幾個象徵性的中心點。
首先,先決定要有幾個「中心點」,這裡假設我要有\(k\)個好了,接下來先隨機給這些「中心點」一個初始的位置,接下來根據數據的靠近程度開始歸類,如果一筆數據比較所有的「中心點」後發現離「中心點」A是最近的話,那這筆數據就歸「中心點」A了,就用這樣的規則把所有數據都做分類。
分完類後,接下來平均每一個資料群體裡的數據座標找出新的代表這個群體的「中心點」,然後又拿這個新的「中心點」根據數據的靠近程度再歸類一次,如此循環多次,直到收斂為止。這樣的話,這\(k\)個「中心點」收斂後會各自佔據四方,並且代表某個群體的中心點。我們就可以找到代表性的\(k\)個點,並拿這些點做「k Nearest Neighbor RBF Network」。
One-Hot Encoding
討論這麼久的ML,我們還沒有討論過假設遇到「類別」要怎麼處理!
通常遇到類別的狀況,我們還是需要把它轉換成數值或向量來處理,常見的方法叫做One-Hot Encoding。
舉個例子,如果要描述血型應該要怎麼做?我們可是無法拿字串下去Regression的啊~此時就需要One-Hot Encoding,假設血型有A, B, AB, O四種,我們可以這樣設定,
\(A = [1, 0, 0, 0]^T\)
\(B = [0, 1, 0, 0]^T\)
\(AB = [0, 0, 1, 0]^T\)
\(O = [0, 0, 0, 1]^T\)
就是這麼簡單,這個動作就叫做One-Hot Encoding。
Matrix Factorization
那如果今天我的Input和Output都是類別,而我們想要讓機器自己去找到匹配Input和Output的機制,解決這個問題的方法稱之為Matrix Factorization。
Matrix Factorization精神上有點像是Autoencoder,Autoencoder找出隱含在Data裡的特性,而Matrix Factorization則是找出隱含的匹配關係。
舉個例子,如果Netflix有了一堆用戶和他們曾看過的電影的資料,我們想要從中抽取出用戶與他愛看的電影之間的關係,所以這不單單只是匹配而已,單純匹配就只需要硬碟就做的到了,我們要做的是找出匹配的規律,並且用更少、更精簡的方式表示這個匹配關係,舉個例子,有可能有部分用戶會被歸納到愛看恐怖片的,並且同時這些客戶會被連結到具有恐怖元素的電影,我們預期Matrix Factorization會有自行歸納整理的能力。
可以仿造Autoencoder來設計Matrix Factorization,而你會發現Activation Function只要使用線性就已經足夠了,因為對於One-Hot Encoding的類別來說,只有一條通道是有效的,這已經具有開關的味道了,所以我們不用在Activation Function上面再弄一道開關,所以採用Linear就足夠了。
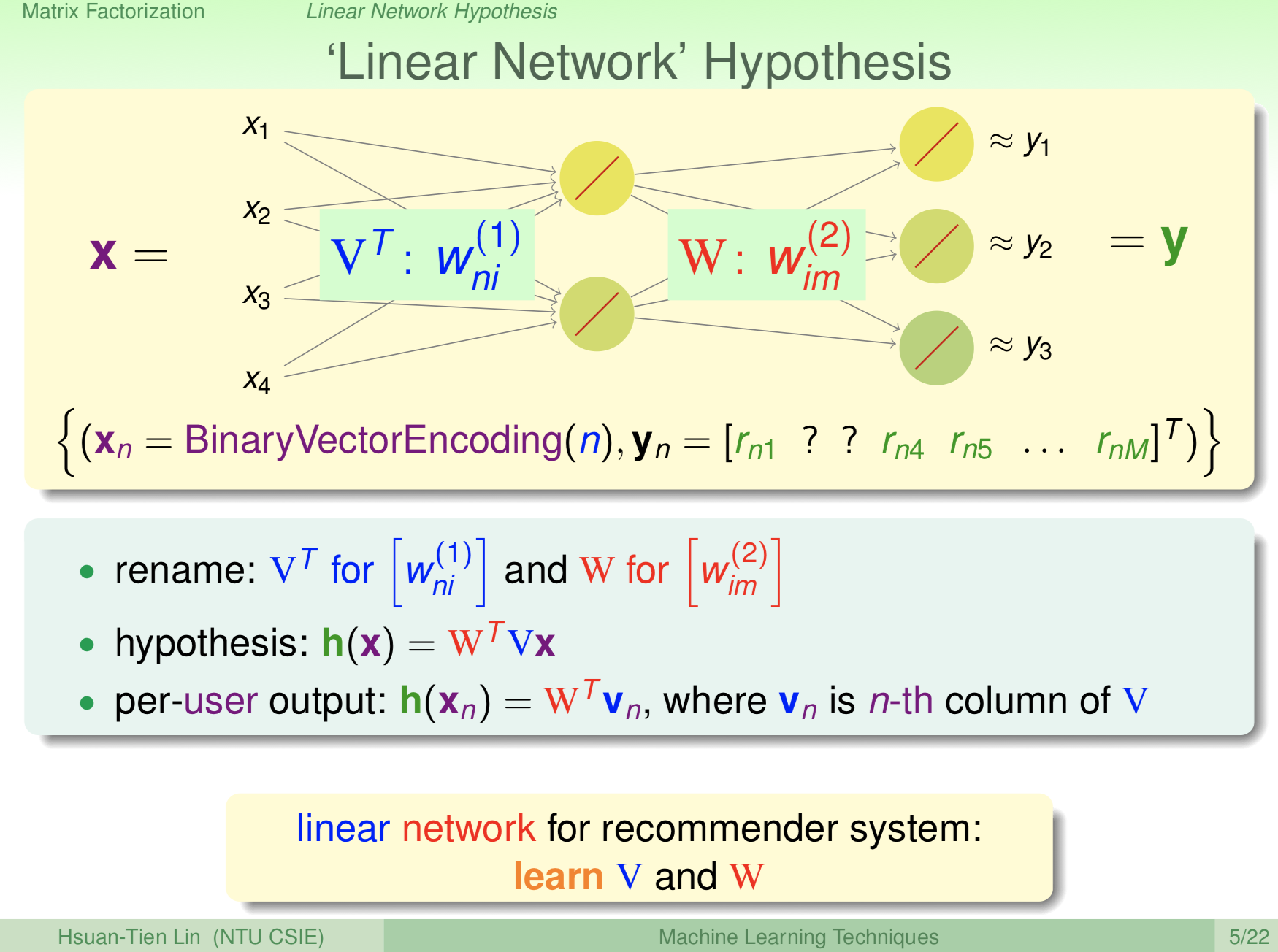
from: https://www.csie.ntu.edu.tw/~htlin/course/mltech17spring/doc/215_handout.pdf
因為是線性模型的緣故,我們可以很簡單的使用矩陣來描述,
Hypothesis: \(h(X) = W^TVX\)
而如果是某一用戶,則
\(h(X_n) = W^TV_n\)
對某個用戶而言與他匹配的電影是一個向量,上面紀錄了他看過的電影,假設我再指定一部電影\(m\),此時\(W_m^T V_n\)就代表這個用戶有沒有看過這部電影。
用這個方法來想問題,假設今天你把用戶和電影填成一個大的表格,或是矩陣,有交集的部分就打個勾,這個矩陣的每個元素表示成\(r_{nm}\),有打勾的部分\(r_{nm}=1\),沒打勾的部分\(r_{nm}=0\),那我們做的轉換W和V最終就是為了讓
\(W_m^T V_n ≈r_{nm}\)
為了評估匹配的好壞,我們定義Error Function為
\(E_{in}(\{W_m\},\{V_n\}) = (1/𝚺_m |D_m|)×𝚺_{n,m} (r_{nm}-W_{m}^TV_n)^2\)
最佳化Matrix Factorization有兩個演算法,一個是Alternating Least Squares,另外一個是SGD。
Alternating Least Squares for Matrix Factorization

from: https://www.csie.ntu.edu.tw/~htlin/course/mltech17spring/doc/215_handout.pdf
第一個方法是利用Linear Regression交互的優化\(W_m\)和\(V_n\),我們的目標是使得\(W_m^T V_n =r_{nm}\),這式子可以用兩個角度看,如果固定\(W_m\),優化\(V_n\),那就是線性擬合\(\{V_n, r_{nm}\}\)的問題;那如果固定\(V_n\),優化\(W_m\),這就是線性擬合\(\{W_{m}, r_{nm}\}\)的問題。因此,交替優化\(W_m\)和\(V_n\)就可以使得\(W_m^T V_n\)越來越接近\(r_{nm}\)了。
SGD for Matrix Factorization

from: https://www.csie.ntu.edu.tw/~htlin/course/mltech17spring/doc/215_handout.pdf
第二個方法則是老招—Gradient Descent,這裡採用隨機的版本SGD,所以過程中我們會隨意的從\((n,m)\)中挑點,然後根據Error Measure
我們就可以得到更新\(W_m\)和\(V_n\)的方法,詳細的方法見上圖所示。
目前,SGD方法是處理大型Matrix Factorization最流行的作法。
結語
本篇介紹類似Neural Network的兩種Network結構,分別為Radial Basis Function (RBF) Network和Matrix Factorization。
在做RBF Network時,我們先找出幾個代表的中心,並評估一筆資料與這些中心的距離,再來再考慮不同中心對於答案的貢獻,加總起來可以預測這筆資料的答案,我們可以使用K-Means的方法來找出k點代表性的中心點來做RBF Network。
Matrix Factorization和Autoencoder有點類似,Autoencoder目標在於找出隱含在Data裡的特性,而Matrix Factorization則是找出隱含的匹配關係,並且介紹了兩種Matrix Factorization的演算法:Alternating Least Squares和SGD方法。
這系列的介紹文章,到這裡算是走到尾聲了,最後跟大家推薦一下老師的最後一堂課的投影片:
https://www.csie.ntu.edu.tw/~htlin/course/mltech17spring/doc/216_handout.pdf
這個投影片裡頭林軒田教授用心的彙整了一整個學期的內容,很值得一看。