機器學習技法 學習筆記 (4)：Basic Aggregation Models

綜觀Aggregation Models

如果今天我有很多支的Model，我有辦法融合他們得到更好的效果嗎？

這就是Aggregation Models的精髓，Aggregation Models藉由類似於投票的方法綜合各個子Models的結果得到效果更好的Model。換個角度看，你可以把整個體系看成一個新的Model，而原本這些子Models當作轉換過後的新Features，所以Aggregation Model裡頭做了「特徵轉換」，這個特徵轉換產生出許多有預測答案能力的Features，稱為Predictive Features，然後再綜合它們得到最後的Model。

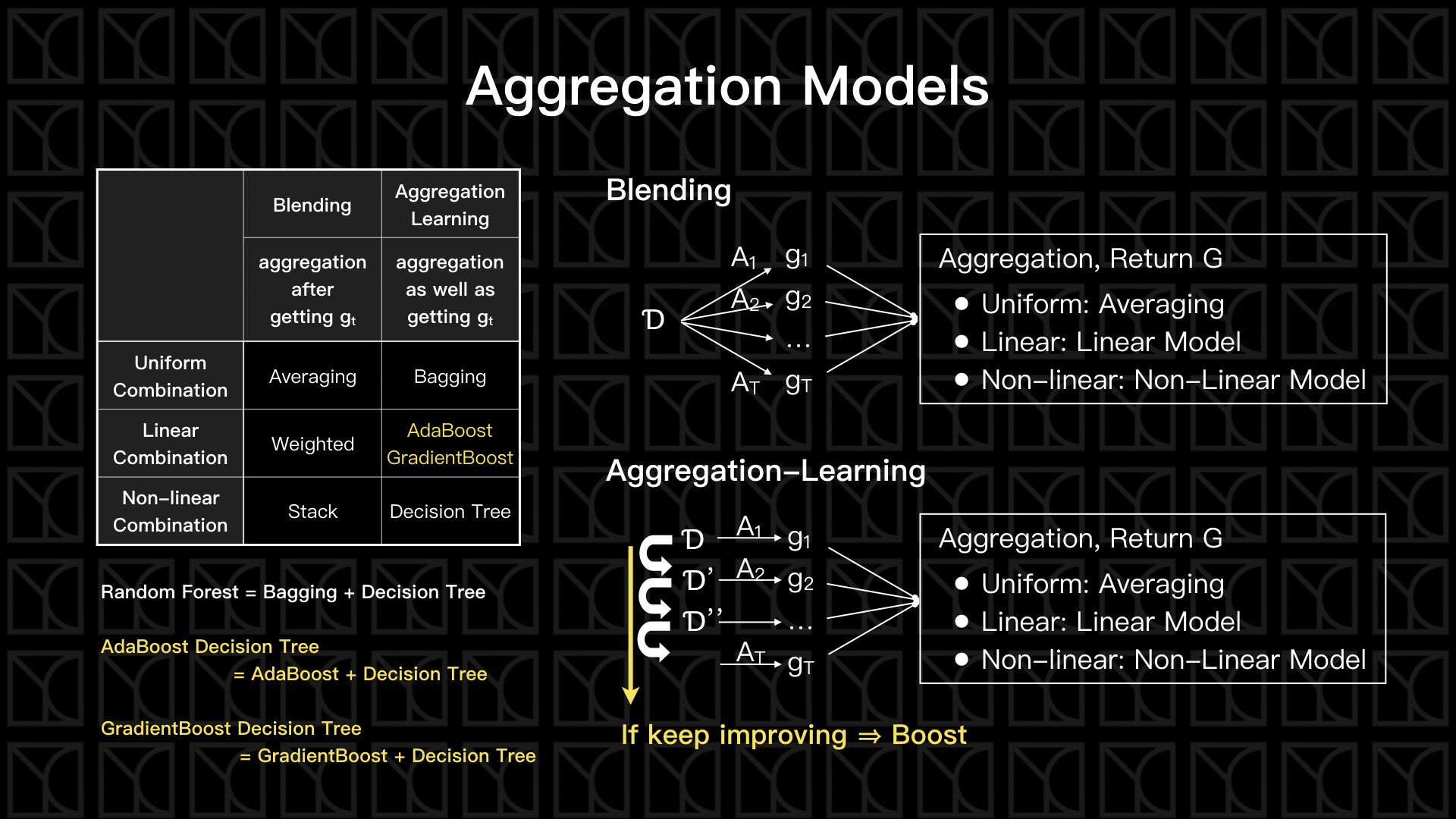
Aggregation Models可以分成兩大類，第一種的作法比較簡單，先Train出一個一個獨立的Predictive Features，然後在綜合它們，「集合」的動作是發生在得到Train好的Predictive Feature之後，這叫做「Blending Models」；第二種作法則是，「集合」的動作和Training同步進行，這叫做「Aggregation-Learning Models」，Aggregation-Learning Models有一個特殊的例子叫做Boost，翻開字典查Boost的意思是「促進」，在這邊的意義是假設在Training過程所產生的Predictive Feature朝著改善Model的方向前進就叫做Boost。

從「集合」的方法上也可以進一步細分三種類型，有票票等值的「Uniform Aggregation Type」，有給予Predictive Features不同權重的「Linear Aggregation Type」，甚至還可以用條件或任意Model來分配Predictive Features，這叫做「Non-linear Aggregation Type」。

所以兩種類型、三種Aggregation Type，交互產生各類的Aggregation Models。有Blending的三種Aggregation Type，Aggregation-Learning的Uniform Type—Bagging，再加上Aggregation-Learning的Linear Type兩種—AdaBoost和GradientBoost，這兩種也亦是Boost的方法，AdaBoost負責處理Classification的問題，而GradientBoost則負責處理Regression的問題，最後介紹Aggregation-Learning的Non-Linear Type—Decision Tree。然後接著，使用Decision Tree結合其他方法再進一步的產生Random Forest、AdaBoost Decision Tree和GradientBoost Decision Tree。

我將會分兩篇來介紹Aggregation Models，一篇介紹沒Boost的部分，就是今天這一篇，另外一篇則是來專攻有Boost的部分。

Blending

Blending是泛指在Training結束之後得到幾個Predictive Features，然後再對這些Predictive Features做集合的方法。

如上圖，基本流程是這樣的，一開始先把Data切成一部分拿來Training，另外一部分拿來Validation，這部份很重要，因為我們待會要利用Validation的Error來決定每筆Predictive Feature對Model的貢獻分配比重；接下來使用不同的方法來產生不同的Predictive Features \(g_{t}\)，來源可能是不同的Model形式、不同的參數變化、不同的隨機情形等等；有了各類的\(g_{t}\)之後，我們就可以選擇使用怎樣的方式來結合它們，如果是Uniform Combination，就直接平均所有\(g_{t}\)就可以了，那如果是Linear Combination，想當然爾就是使用線性模型來結合，那如果是Non-Linear Combination，你可以使用任意Model來描述也行；決定好結合方式了，也就同時決定了「特徵轉換」的方法，接下來出動Validation Data，使用這個「特徵轉換」來轉化Validation Data並且做Fitting，最後我們會找到一組解最佳的參數來確定結合的方法，如果是Uniform Combination是不需要這一步的，基本上你得到\(g_{t}\)就直接平均就得到結果了，而Linear Combination則是需要去找出\(α_{t}\)。

在數學上可以證明Aggregation的效果會比單一一個\(g_{t}\)的描述的結果還好，這很像是在做投票選舉，不同方法可能帶有不一樣的偏見，但是綜合所有意見之後可以找到共識，這個共識是具有較少偏見的，你可以想像偏見就像是Overfitting，所以Aggregation是具有像Regularizaiton一般抑制Overfitting的效果的，但有些時候特別的看法不一定是偏見，也許這一個方法可以看出其他方法看不出來的規律，此時這個部分也不會被完全忽略掉，所以Aggregation也可以同時擁有像Feature Transform一樣的複雜度。因此Aggregation的方法可以同時增加Model複雜度又同時防止它Overfitting，這個效果是我們以前沒看過的，所以我們會說Aggregation具有截長補短的效果。

Bagging

Bagging是一種利用變換原本Data來造出不同\(g_{t}\)的簡單方法，Bagging的全名稱為Bootstrap Aggregation，其中Bootstrap指的是「重新取樣原有Data產生新的Data，取樣的過程是均勻且可以重複取樣的」，使用Bootstrap我們就可以從一組Data中生出多組Dataset，然後就可以使用這些Dataset來產生多組\(g_{t}\)，最後再Uniform Combination這些\(g_{t}\)，就完成了Bagging。

Decision Tree（決策樹）

接下來談Decision Tree這個重要的概念，Decision Tree其實就像是一個多層次的分類，每一次的分類會根據某一個Feature來當作依據判斷它應該繼續往哪一條路走，然後繼續使用可能是另外一個Feature來繼續細分下去。舉個例子好了，假設今天有一個自由式摔跤重量63公斤的女選手Ms. D要參加奧運，所以得透過奧運的分級制度分級，一開始可能根據比賽模式這個Feature下去分類，我查了一下有自由式和古典式兩種，所以Ms. D會被歸類到自由式，再來根據性別這個Feature下去分類，Ms. D是女選手所以分到女選手這一類，再繼續可能會根據體重來細分，體重在奧運分級共有8級，Ms. D可能就被分到62公斤级的那類，這樣的分類精神就是Decision Tree。

所以，Decision Tree的優點是結果所提供的結構非常容易讓人了解，另外在演算法部分也很容易實現，而且因為具有以條件篩選的結構，所以其實很容易可以做到多類別分類。但是Decision Tree也有一些為人詬病的缺點，Decision Tree整體理論是缺乏基礎的，存在很多是前人的巧思，很多作法都是使用起來感覺效果不錯就延續下去了，目前並不了解背後的原因，也因此沒有一個代表性的演算法存在。

在講Decision Tree操作方法之前應該要先來講一下Decision Stump，Decision Stump做的事其實就是上述中提到的對某個Feature做切分的這件事，可以想知Decision Stump是一個預測效果很差的Model，而Aggregation這些Decision Stump形成Decision Tree卻有很好的效果，這就是Aggregation的威力。

見上圖，我們來看一下Decision Tree的流程，Decision Tree最為人所知的演算法是C&RT，C&RT是一整套的套件，我們今天只是提到它整套套件中的一種特例。Decision Tree產生的函式是這樣的，一開始先判斷進來的這筆資料還能不能繼續分支下去，在三個情況下，我們沒辦法繼續分支下去：

1. 數據\(Ɗ\)只剩一筆數據。
2. 這群數據\(Ɗ\)已經最佳化了，我們會說它的Impurity=0，這個時候我們不知道要從哪裡再切一刀。
3. 這群數據\(Ɗ\)的Feature \(X_{n}\)都完全相同。

當無法再繼續分支下去時，會回傳一個\(g_{t}(x)=constant\)，這個常數是一個可以使得這個群體內\(E_{in}\)最小的數值，在分類問題中這個常數是\(\{y_{n}\}\)中佔多數的類別，在Regression問題中這個常數是\(\{y_{n}\}\)的平均值。

大家應該會有點驚訝，Decision Tree也有辦法做Regression？其實是可以的，我們只要讓群裡頭的數字作平均當代表，這們一來要處理實數問題也是可以做到的，不過我們會預期處理Regression問題時會切的比Classification問題來的細和多層。

那接下來來看假如還可以繼續分支下去應該要怎麼做，這邊假設我們只切一刀分為兩個區塊\(C=2\)，我們該根據怎樣的條件來切呢？我們剛剛其實有稍微提到，那就是Impurity，我們可以根據Impurity Function來衡量「一群資料的不相似程度」。

分類問題的Impurity Function有以下兩種：

• \(Impurity(Ɗ) = (1/N) 𝚺_{n} ⟦y_{n}≠y^*⟧\)，其中\(y^*\)是\(Ɗ\)中佔多數的類別，這個衡量方法就直接的去數出錯誤答案的比例。
• Gini Index: \(Impurity(Ɗ) = 1 - 𝚺_{k} [ 𝚺_{n}⟦y_{n}=k⟧ / N ]^{2}\)，Gini Index是最為流行的作法，它不同於上一個作法，它是在評估所有的類別後才去計算Impurity，其中 \(k\) 代表類別。

而Regression問題有以下方法：

• \(Impurity(Ɗ) = (1/N) 𝚺_{n} ( y_{n} - \overline{y} )^{2}\)，其中\(ȳ\)代表的是\(\{y_{n}\}\)的平均值，式子中使用平方誤差來評估資料的離散程度。

有了Impurity Function我們就有了指標，找出應該要使用哪個Feature、應該要怎麼切，才能使得Impurity Function總和最小，決定好這一刀後，接下來就從這一刀切下去，把Data一分為二，然後這兩組Data再各自去長出一棵Decision Tree，經過遞迴式的迭代，我們就可以得到一棵完整的Decision Tree了。

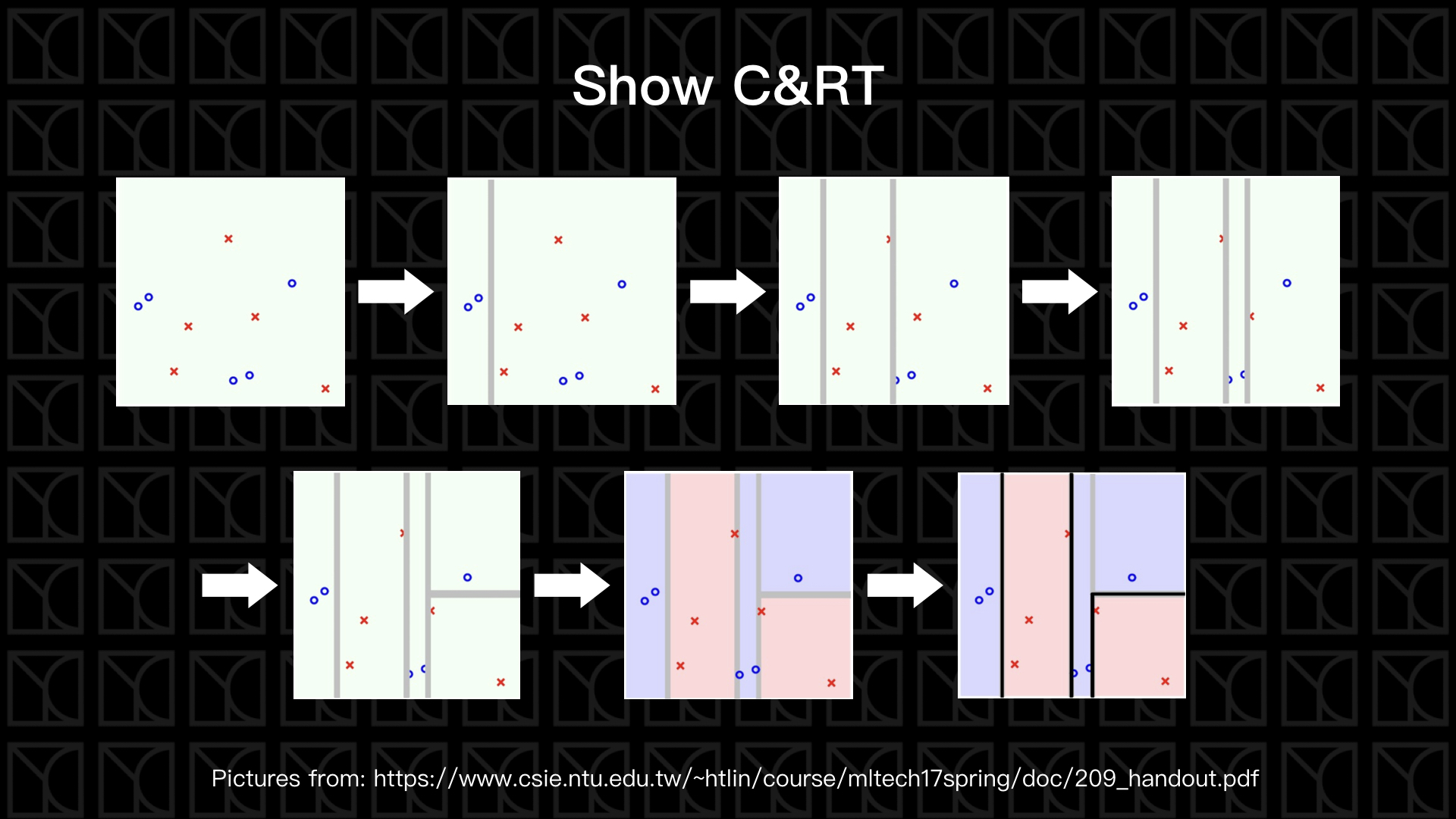
如果我們讓一棵樹完整的長成了，可以想到的後果想當然爾就是Overfitting，所以我們必須要做Regularization，Decision Tree常用的Regularization的方法是Pruning，就是砍樹，我們將分支的數量\(Ω(G)\)加進去\(E_{in}\)中做為Regularization，所以我們問題變成是去找到 \(argmin\ E_{in}(G)+λΩ(G)\)，其中的λ可以利用Validation Data來做選擇，你會發現如果真正的要去找到\(argmin\ E_{in}(G)+λΩ(G)\)的最佳解，這問題會非常的困難，因為你必須要把所有的可能的樹都考慮進去，所以有一個替代方案，我們可以先將樹整棵長完，然後在一一的去合併分支，看哪兩個分支合併之後可以使\(E_{in}\)最小就先合併，使用這樣的作法逐步減少分支的數量。

順道一提，C&RT可以產生許多替代方案，這些替代方案稱為Surrogate Branch，當有一筆Data缺乏某個Feature，我們仍然有辦法使用替代方案來做決策，這是C&RT的一個大大的優點。

Random Forest（隨機森林）

如果我拿Decision Tree來做Bagging這樣可以嗎？當然OK，Aggregation Model的精髓就是可以綜合子Model，那Decision Tree也可以是看成一個子Model，所以我們在做的就是Aggregation of Aggregation，這種拿Decision Tree來做Bagging的Model叫做Random Forest，這個名字取的很生動，有很多棵數的地方就是森林啦！

Decision Tree和Bagging其實是有互補的作用，Decision Tree這種演算法是「變異度」很高的，因為它不像SVM這類的演算法，會去評估與Data之間的距離，空出最大的距離來避免Overfitting，而Bagging正可以拿來減少「變異度」，消除雜訊，所以Random Forest會比Decision Tree更不易Overfitting。

見上圖，我們來看一下Random Forest的流程，一開始先做和Bagging裡頭一樣做的事Bootstrap，藉此來產生新的Dataset，另外為了讓我們隨機程度變得更高，我也對我們Features來做點變化，將它乘上一個亂數產生的\(P\)，如果\(P_{i}=0\)代表我們完全不取這個Feature，如果\(P_{i}=1\)代表我們完全取這個Feature，我們更可以以分數來代表我們對某個Feature的重視程度，這個手法叫做Random-subspace。接下來就是把弄的很亂的Dataset放進去長一顆Decision Tree，最後再把所有的Decision Tree平均就是Random Forest的結果。

Random Forest發展出了一套獨特的Validation方法，我們知道Bootstrap的結果會造成有些Data取用而有些Data不使用，而取用的Data會拿來Training，這讓你想到什麼呢？沒錯，沒有用到的Data可以做Validation，我們可以拿那些沒有被取用的Data來評估Training的好壞，我們會稱那些沒被取用的Date叫做Out-of-Bag Data，而利用Out-of-Bag Data來Validation的Error，稱為Out-of-Bag Error，

Out-of-Bag Error \(E_{oob}=(1/N) 𝚺_{n} err(y_{n}, {G_{n}}^{-}(x_{n}))\)

\(where:\ {G_{n}}^{-}(x) = Average(Models\ without\ using\ this\ data)\)

Out-of-Bag Error提供一個很方便的Self-validation的方法。

在以前Linear Model中，權重W代表每筆Feature對Model的貢獻度，我們可以由W的分量大小來評估每個Feature的重要程度。Random Forest則是可以利用\(E_{oob}\)和Random-subspace來標示出每個Feature的重要程度，想法是這樣的，如果今天某一個Feature i 對Model很重要，所以說我只對Feature i 做Random-subspace，也就是只有\(P_{i}\)是隨機的，可以想知\(E_{oob}\)會大幅增加，因此利用這個想法我們可以用來定義Feature的重要程度，

結語

在這一篇我們提了幾個基礎的Aggregation Models，從最簡單的Blending，Blending的方法本身不去產生子Model，而是使用兩階段學習，先自行挑選和訓練來產生很多的子Model，而Blending只在這些結果上做不同方式的結合。

接下來，Learning-Aggregation的方法則化被動為主動，我們先提了Bagging，裡頭使用Bootstrap的技巧來造成資料的隨機性，利用這樣的變異來產生多個\(g_{t}\)，再接下來我講了Decision Tree，Decision Tree由多個Decision Stump組合而成，每個Decision Stump就是\(g_{t}\)，Decision Tree做的事就是，產生Decision Stump、切分Dataset、再產生Decision Stump...接續下去，最後綜合全部的Decision Stump成為Decision Tree。

最後，我們結合Decision Tree和Bagging產生了Random Forest，利用彼此的互補，讓效果變得更好可以比單純Decision Tree更好。