機器學習基石學習筆記 (3)：機器可以怎麼樣學習?

Posted on August 07, 2016 in AI.ML. View: 7,667

前言

在上一回中，我們已經了解了機器學習在理論上有怎樣的條件才可以達成，所以接下來我們就可以正式的來看有哪一些機器學習的方法。

在這一篇中，我會帶大家初探：機器可以怎麼樣學習? 內容包括：Gradient Descent、Linear Regression、Logistic Regression、使用迴歸法做二元分類問題等等。

Gradient Descent（梯度下降）

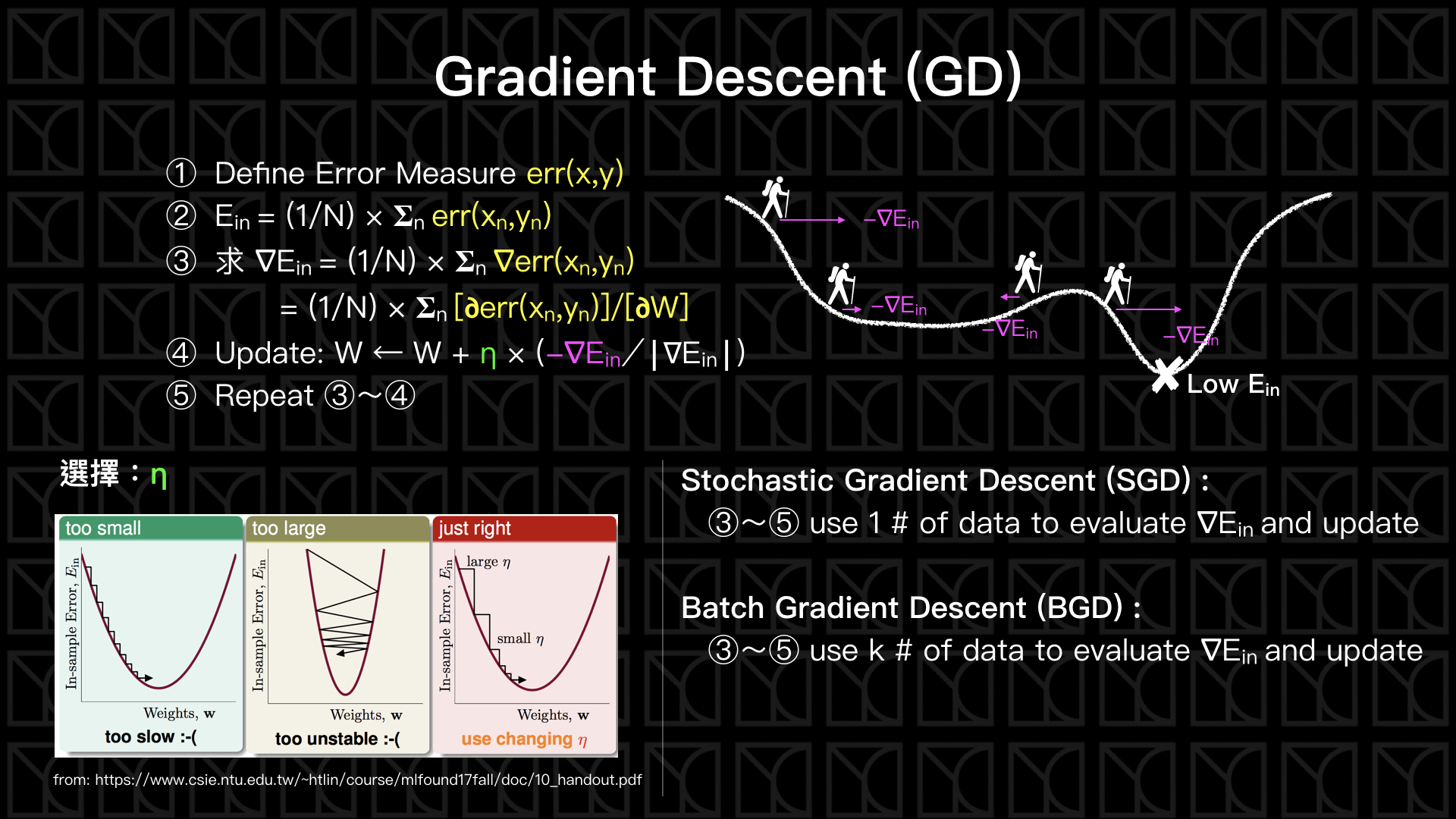
還記得上一回我們歸納出了一套ML的流程，複習一下

準備好足夠的數據
把Model建立好，$d_{VC}$必須要是有限的，而且大小要適中
定義好評估$E_{in}$的Error Measurement
使用演算法找出最佳參數把$E_{in}$降低
最後評估一下是否有Overfitting的狀況，確保$E_{in} \approx E_{out}$

請容許我先不管Model這部份該怎麼建立，我們先來看如何找到最佳參數這部份，假設今天我知道$E_{in}$的評估方法，我該如何找到最佳的參數來使得$E_{in}$更小？有一套普遍的方法叫做Gradient Descent，很強大，甚至連現今流行的「深度學習」找最佳解的機制也是從Gradient Descent衍生出來的。

想像一下你是一位登山客，你在爬一座由$E_{in}$所決定的高山，你的目標是去這座山最低的山谷，也就是$E_{in}$最小的地方，因為村莊正在那裡，但是很不幸的你沒有地圖，這個時候有什麼方法可以知道低谷在哪裡呢？最簡單的答案就是一直下坡就對啦！反正我知道村莊在山谷裡，那我就一路下山應該就可以找到村莊了，這就是Gradient Descent的精髓。

在數學上有一個衡量函數變化的東西，這就是Gradient（梯度），Gradient是一個向量，它的「方向」指向函數值增加量最大的方向，而它的「大小」反應這個變化有多大，其實就是一次微分啦！只不過Gradient推廣到高維度而已。所以我們和這個登山客做一樣的事情，我們朝著下降最多的方向前進，這就是Gradient Descent（梯度下降法），我剛剛說了，梯度是指向函數值增加量最大的方向，那顯然我們往反方向走就可以達到最大下降，所以如果我們有一個Error函數$E_{in}$，它的Gradient就是$\nabla E_{in}$，那我們的下降方向就是$- \nabla E_{in}$。

來看一下上圖中Gradient Descent的流程，

定義出Error函數
Error函數讓我們可以去評估$E_{in}$
算出它的梯度$\nabla E_{in}$
朝著$\nabla E_{in}$的反方向更新參數W，而每次只跨出$η$大小的一步
反覆的計算新參數$W$的梯度，並一再的更新參數$W$

這邊要特別注意，流程中的第四項中，有提到$η$，$η$稱為Learning Rate，它影響的是更新步伐的大小，$η$的選擇要適當，如果$η$太小的時候，我們可能要花很多時間才可以走到低點，但如果$η$太大的話，又可能導致我們在兩個山腰間跳來跳去，甚至越更新越往高處跑，所以選擇適當的$η$相當的重要，所以下次如果你發現$E_{in}$一直降不下來甚至在增大，試著將$η$減小看看。另外$η$也可以不是定值，我們可以直接設$η＝|\nabla E_{in}|$，這麼一來遇到陡坡的時候它就會跨大一點的步伐，遇到緩坡的時候就會跨小步一點，隨狀況調整$η$的值。

Gradient Descent (GD, 梯度下降) 有兩個變形，分別為Stochastic Gradient Descent (SGD, 隨機梯度下降) 和 Batch Gradient Descent (BGD, 批次梯度下降)，這差別只在於評估$\nabla E_{in}$的時候所考慮的Data數量，正常來說必須要考慮所有的Data，我們才會得到真正的$E_{in}$，才有辦法算出正確的$\nabla E_{in}$，但這樣所要付出的代價就是較大的計算量。

所以Stochastic Gradient Descent的作法是一次只拿一筆Data來求$\nabla E_{in}$，並且更新參數$W$，這樣的更新方法顯然會比較不穩定，但我們假設，經過好幾輪的更新後，已經完整看過整個數據了，所以平均來說效果和一般的Gradient Descent一樣。

另外還有一種介於Gradient Descent和Stochastic Gradient Descent之間的作法，稱之為Batch Gradient Descent，它不像Stochastic Gradient Descent那麼極端，一次只評估一組Data，Batch Gradient Descent一次評估k組數據，並更新參數W，這是相當好的折衷方案，平衡計算時間和更新穩定度，而且在某些情形下，計算時間還比Stochastic Gradient Descent還快，為什麼呢？GPU的計算方法你可以想像成在做矩陣計算，矩陣元素在計算的時候往往是可以拆開計算的，此時GPU利用它強大的平行化運算將這些元素平行計算，可以大大增進效率，所以如果一次只算一筆資料，反而是沒有利用到GPU的效率，所以如果你用GPU計算的話，依照你的GPU去設計適當的k值做Batch Gradient Descent，是既有效率又穩定的作法。

Gradient Descent求最佳解其實不是完美的，還記得我們的目標嗎？我們希望可以走到最低點的山谷裡，所以我們採取的策略是不斷的下降，這個時候如果遇到兩種情形就會導致還沒到山谷就已經動彈不得，

小山谷，數學上稱為Local Minimum，雖然在那點看起來，那邊的確是相對的低點，所以$\nabla E_{in}=0$，但卻不是整個$E_{in}$的最低點，但也因為$\nabla E_{in}=0$的關係，更新就不會再進行。
平原，數學上稱為Saddle Point（鞍點），在一片很平的區域，$\nabla E_{in}=0$，所以就停止不動了。

針對這些問題有一些改良後的演算法，在這裡不詳述，請參考S. Ruder的整理。

好！我們已經了解了怎麼使用Gradient Descent去找到$E_{in}$最小的最佳參數，那我們可以回頭看Model有哪一些？Error Measure該怎麼定？

Linear Regression

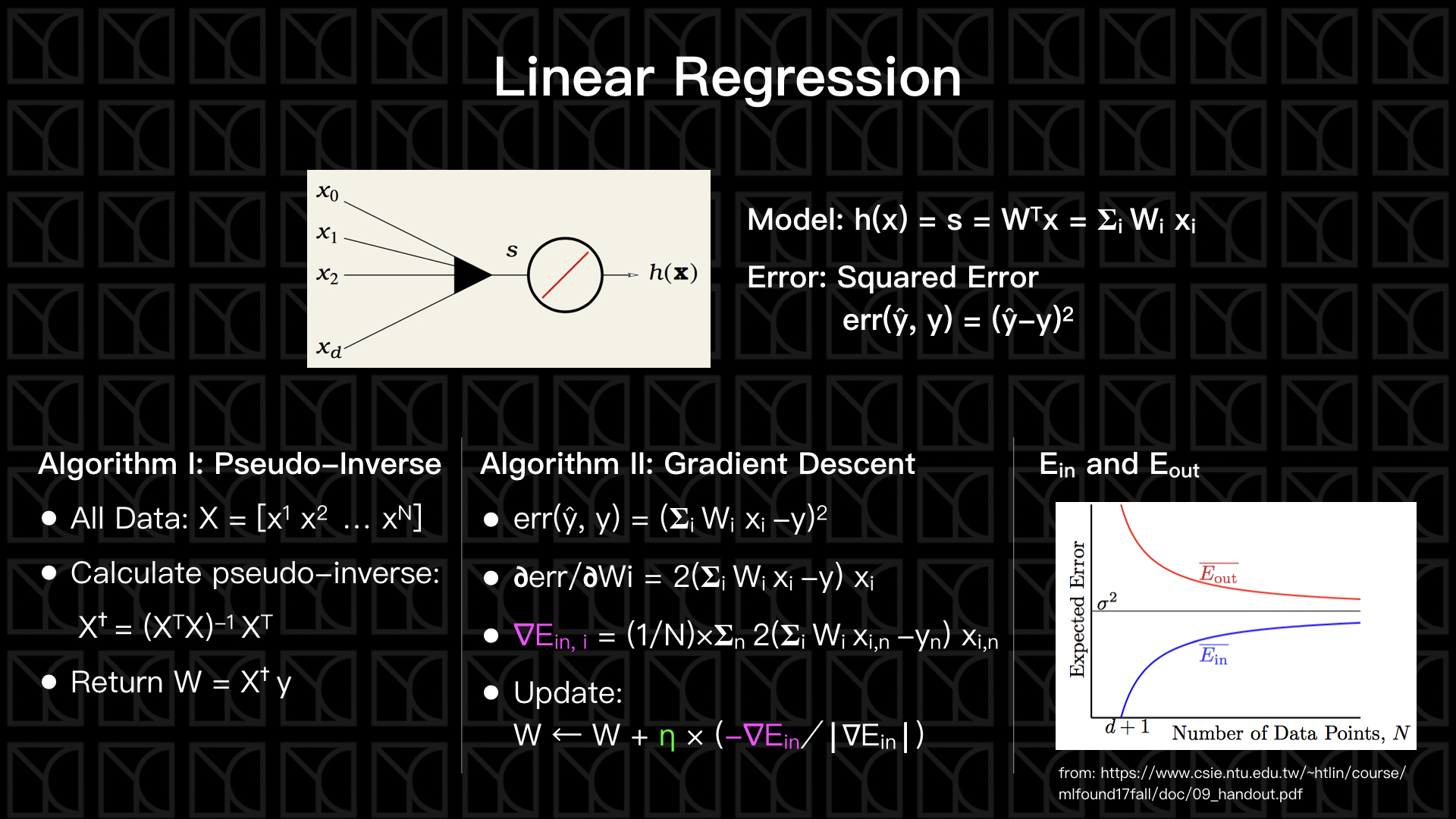
先從最簡單的看起，那就是線性迴歸（Linear Regression），假設今天我要用三種變數$(x_1, x_2, x_3)$來建立一個簡單的線性模型，那就是

$$ w_0+w_1 x_1+w_2 x_2+w_3 x_3 $$

這個又稱為Score，標為$s$，為了方便起見，我們會額外增加$x_0=1$的參數，這麼一來Score就可以寫成矩陣形式

$$ s = w_0 x_0+w_1 x_1+w_2 x_2+w_3 x_3=W^T x $$

$$ where: W = [w_0, w_1, w_2, w_3], x = [x_0=1, x_1, x_2, x_3] $$

在線性模型中，這個 s 就正好是我們Model預測的值，通常我們會把預測得來的 $y$ 記作$\widehat{y}$ (y hat)，如果今天這個 y 和 ŷ 是實數的話，那這就是一個標準的Linear Regression問題，那如何去衡量預測的好或不好呢？我們可以使用Squared Error來衡量，$err(\widehat{y},y)=(\widehat{y}-y)^2$，所以 $\widehat{y}$ 和 $y$ 越靠近Error就越小。

Squared Error的$E_{in}$平面是一個單純的開口向上的拋物線，所以它的最低點其實是有解析解的，我們可以靠著數學上的Pseudo-Inverse方法把最佳參數給算出來，但是Pseudo-Inverse計算非常龐大，當數據量很大時這個方法是不可行的，而剛剛介紹的Gradient Descent計算複雜度只有$O(N)$。

Logistic Regression

在上一回討論二元分類問題時，我們的評估模型都是非黑即白的

在上一回討論二元分類問題時，我們考慮的狀況是「沒有雜訊」的情形，不過在實際情況下，「雜訊」是一定需要考慮的。在「沒有雜訊」的情形下，一筆Data只會有一個確定的答案要嘛是 $- 1$ 不然就是 $+ 1$，如果考慮「雜訊」，一筆Data出現的答案可能呈現機率分布，介於 $- 1$ 和 $+ 1$ 之間，舉例可能會產生像下面一樣的情況，

$$ \mathbb{P}(◯|X^{(1)}) = 0.9,\ \mathbb{P}(✕|X^{(1)}) = 0.1 $$

之前PLA的分類方法是屬於非黑及白的，預測的結果不存在模糊地帶，這種分類法我們稱為Hard Classification，這種分類法並不能描述機率分布，所以我們來考慮另外一種分類法，稱之為Soft Classification。

Soft Classification看待每個答案不是非黑及白的，而是去評估每個答案出現的機會有多大，以此作為分類，我們打算使用Regression的連續特性來產生Soft Classification，我們需要引入一個重要的函數—Logistic Function，這個函數可以將所有實數映射到0到1之間，如上圖下方中間的圖示所示，Logistic Function會將極大的值映射成1，而將極小值映射成0，這個0到1的值剛剛好可以拿來當作機率的大小。

所以我們就可以來建立一個有機率概念的模型，這個Model的預測值是一個機率，一樣的先給予輸入變數$x$和權重$W$求出Score $s$，再把 $s$ 放到Logistic Function當中，我們就可以映射出在一個機率空間，我們藉由調整$W$來改變Model來擬合我們的Data，有了這個新的Model，我們就可以用機率的方式來描述二元分類，

$$ \mathbb{P}(◯|X^{(1)}) = Θ(s) $$

$$ \mathbb{P}(✕|X^{(1)}) = 1 - Θ(s) = Θ(-s) $$

$$ where:\ Θ(s)=1/[1+e^{-s}] $$

OK! 決定好Model，我們就可以來定義它的Error Measurement的方式了，這個時候如果使用Squared Error來作為Error Measurement你會發現這種評估方式有一點失焦了，如果採用Squared Error，我們做的事是將機率的值給擬合精準，但我們知道這個機率的產生是來自於雜訊，預測雜訊是沒有意義的，要做的事應該是要在考慮雜訊之下盡可能提升模型會產生取樣資料的可能機率。

這就是Max Likelihood的概念，

$$ \mathbb{P}(likelihood) = \mathbb{P}(x^{(1)})\mathbb{P}(◯|x^{(1)},H) \times \mathbb{P}(x^{(2)})\mathbb{P}(✕|x^{(2)},H) \times … \times \mathbb{P}(x^{(N)})\mathbb{P}(◯|x^{(N)},H) $$

我們的任務就是找一個function set $H$使得我可以最大化likelihood，

$$ argmax_{({H})} \mathbb{P}(likelihood) $$

$$ =argmax_{({H})} \sum_{y^{(n)}\ is\ ◯} \{ln[\mathbb{P}(x^{(n)})]+ln[\mathbb{P}(◯|x^{(n)},H)] \}+ \sum_{y^{(n)}\ is\ ✕} \{ln[\mathbb{P}(x^{(n)})]+ln[\mathbb{P}(✕|x^{(n)},H)]\} $$

$$ =argmax_{({H})} \sum_{y^{(n)}\ is\ ◯} ln[\mathbb{P}(◯|x^{(n)},H)] + \sum_{x^{(n)}\ is\ ✕} ln[\mathbb{P}(✕|y^{(n)},H)] $$

$$ =argmin_{({H})} \sum_{y^{(n)}\ is\ ◯} -ln[\mathbb{P}(◯|x^{(n)},H)] + \sum_{y^{(n)}\ is\ ✕} -ln[\mathbb{P}(✕|x^{(n)},H)] $$

假設 $◯ \equiv (y=+1)$ and $✕ \equiv (y=0)$，則上式可以化簡，得

$$ =argmin_{({H})} \sum_{n} -y^{(n)}ln\mathbb{P}(◯|x^{(n)},H) -(1-y^{(n)})ln[1-\mathbb{P}(◯|x^{(n)},H)] $$

其中$E_{ce}=-yln\mathbb{P}(◯|x,H)-(1-y)ln[1-\mathbb{P}(◯|x,H)]$ 就是Cross-Entropy Error。

而對於logistic regression model而言，$\mathbb{P}(◯|x,H)=Θ(s)$，代入Cross-Entropy Error得

$$ E_{ce,logistic}=-ylnΘ(s)-(1-y)ln(1-Θ(s))=-ylnΘ(s)-(1-y)lnΘ(-s) $$

我們可以使用Gradient Descent來降低Cross-Entropy，這又稱為Logistic Regression，在這個問題中就沒有簡單的解析解可以直接算，只能使用Gradient Descent來求取近似解。

使用迴歸法做二元分類問題

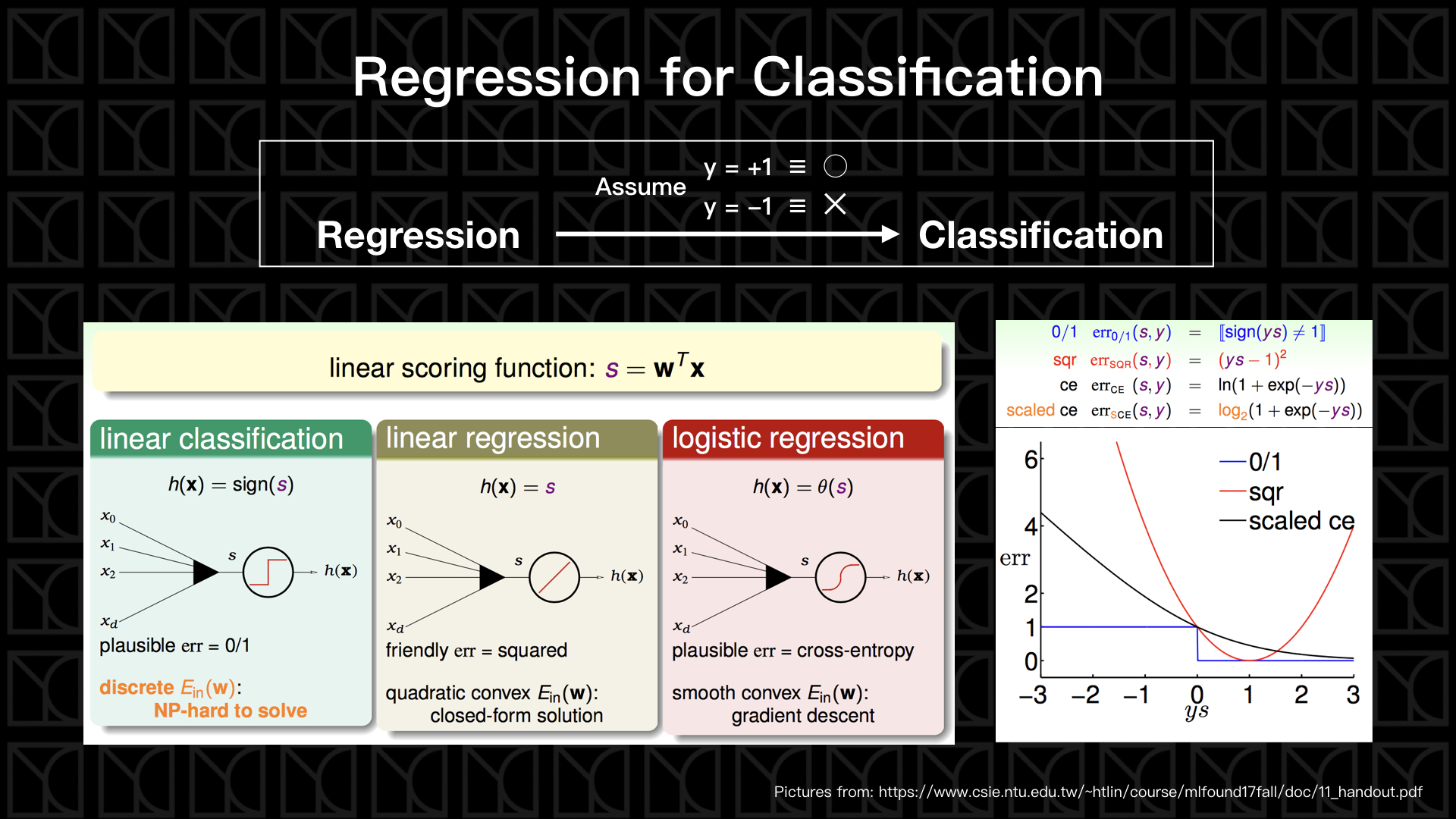
剛剛介紹了Logistic Regression，其實我們是可以將Logistic Regression運用來做二元分類問題。

線性模型的標準方法，我們會將變數$x$做線性組合得到Linear Scoring Function — $s$，線性組合的係數和Threshold稱為權重$W$，我們可以調整權重$W$來改變Model，那針對看待$s$的不同方式就衍生出不同的方法。那為了可以將Regression問題轉換成二元分類問題，所以通常我們會假設$(y=+1)$為$◯$，$(y=-1)$為$✕$。

先回顧一下之前PLA的作法，我們把 $s>0$ 的狀況視為$◯$，也就是$(y=+1)$；然後把$s<0$ 的狀況視為$✕$，也就是$(y=-1)$，把這個概念畫成上圖右側的圖，圖中藍色的階梯函數就是PLA的Error Measurement，正是因為它是一個階梯函數，所以我們不能使用Gradient Descent等Regression方法來處理，因為在階梯的每一點$\nabla E_{in}$都是0（除了原點外），也就是如此PLA在更新的過程才無法確保趨近於最佳解，而需要使用Pocket PLA來解決這個問題。

那如果我們用Linear Regression來做這件事呢？我們把Squared Error畫在上圖右側小圖的紅線，你會發現它的低點會落在$y\times s=1$的地方，這應該不是我們要的結果，雖然它一樣可以把錯誤的判斷修正回正確，但是面對過度確定的正確答案，它反而會去修正它往錯誤的方向，很顯然這不是我們想要的。

最好的方式就是Logistic Regression了，我們將$s$做Logistic Function的轉換，轉換成機率，並在評估最大化Likelihood的條件下定義出Cross-Entropy來當作Error Measurement，在上圖右側的小圖，我們稍微調整Cross-Entropy，使得它的Error Function可以在$y\times s=0$的地方和Squared Error相切，這張圖告訴我們的是隨著Grandient Descent每次的更新，Logistic Regression會把分類做的越來越好。

後話

在這一篇當中，我們介紹了Grandient Descent這一個相當重要的演算法，並且運用在兩種Regression上：Linear Regression和Logistic Regression，Linear Regression是最簡單的Regression方法，甚至它還可以使用Pseudo-Inverse的方法直接算出最佳解，Logistic Regression考慮了有雜訊的Data產生的機率分布，我們可以用Logistic Regression做Soft Binary Classification，而且我們也說明了Logistic Regression為何適合拿來用在二元分類上。本篇我們對於ML的實際作法有了基本認識，在下一篇，我們繼續討論還有沒有什麼方式可以讓ML做的更好。

Previous Post Next Post

前言

Gradient Descent（梯度下降）

Linear Regression

Logistic Regression

使用迴歸法做二元分類問題

後話

You might enjoy